78,884
Пошаговое объяснение:
Для решения данной задачи воспользуемся теоремой синусов. Звучит она так: "Стороны треугольника пропорциональны синусам противолежащих углов.", а выглядит так:
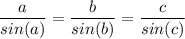 , где a, b, с - стороны треугольника, а sin(a,b,с) - противолежащие углы соответствующих сторон треугольника.
, где a, b, с - стороны треугольника, а sin(a,b,с) - противолежащие углы соответствующих сторон треугольника.
Подставим известные нам значения, а сторону NK возьмем за x :
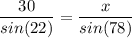
По таблице Брадиса подставляем вместо синусов - числовые значения. Получаем:
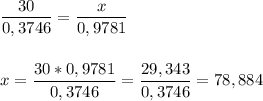
Точное значение получить невозможно, но приближенная длина стороны NK = 78,884
Для наглядности моего решения - прикрепил фото с пояснением.

Пропорция - это верное равенство двух отношений.
6 : 0,2 = 15 : 0,05 6 : 0,2 = 120 : 0,4 6 : 0,2 = 15 : 0,5
6 · 0,05 = 0,2 · 15 6 · 0,4 = 0,2 · 120 6 · 0,5 = 0,2 · 15
0,3 ≠ 3 2,4 ≠ 24 3 = 3
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
6 : 0,2 = -15 : 0,5 5 · 10 = 5 : 0,1
6 · 0,5 = 0,2 · (-15) 50 = 50, но это не пропорция
3 ≠ -3
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
0,5 · 10 = 0,05 · 100 10 : 100 = 0,05 : 0,5 - пропорция
5 = 5, но это не пропорция 100 : 10 = 0,5 : 0,05 - пропорция
10 : 0,05 = 100 : 0,5 - пропорция
0,05 : 10 = 0,5 : 100 - пропорция
ответ: 6 : 0,2 = 15 : 0,5 является пропорцией.
[a,b]int(√(x^2+1) *dx ) =
= b*√(b^2+1)/2 + ln(b+√(b^2+1) )/2 - a*√(a^2+1)/2 - ln(a+√(a^2+1) )/2
Пошаговое объяснение:
[a,b]int(√(x^2+1) *dx )
Замена :
x= ( t- t^-1)/2
Примечание :
(t-t^-1)/2 -монотонно возрастающая функция
dx = dt/2 *( 1 +t^(-2 ) )
x^2+1 = (t^2 -2 +t^-2)/4 +1 = (t^2+2+t^-2)/4 = (t+t^-1)^2 /4
[a,b]int(√(x^2+1) *dx ) = 1/4 * [a,b]int ( dt*(t+t^-1) *(1+t^-2) ) =
= 1/4* [a,b]int ( dt* ( t +2* t^-1 + t^-3 ) = 1/4 [a,b] ( t^2/2 +2*ln(t) - t^-2/2 ) =
= 1/2* [a,b] ( ( (t+t^-1)/2 ) * ( (t-t^-1)/2 ) +ln(t) )
Поскольку :
(t- t^-1)/2 =x
(t+t^-1) /2 =√(x^2+1)
t = x+ √(x^2+1)
[a,b]int(√(x^2+1) *dx ) = [a,b] ( x*√(x^2+1)/2 + ln(x+√(x^2+1) )/2 ) =
= b*√(b^2+1)/2 + ln(b+√(b^2+1) )/2 - a*√(a^2+1)/2 - ln(a+√(a^2+1) )/2