Пошаговое объяснение:
Доказательство:
Минимальное количество спичек, где понятен исход игры:
1(2) спички - Петя начинает и выигрывает;
3 спички - Петя начинает - берёт 1(2) спички, Ване остаётся 2(1) спички - выигрывает Ваня.
Поэтому, смысл игры заключается в том, чтобы выводить соперника
на количество спичек, делящееся на 3 - тогда выигрыш обеспечен.
Следовательно:
а) 9 спичек - начинает Петя и поигрывает, выиграет Ваня.
б) 10 спичек - Петя берёт 1 спичку и Ване остаётся 9 спичек
(делится на 3), то есть Петя выигрывает.
в) 11 спичек - Петя берёт 2 спички, остаётся 9 спичек и Петя выигрывает.
г) 100 спичек - чтобы Петя выиграл. он должен взять 1 спичку,
остаётся 99 спичек (делится на 3) и далее брать столько спичек,
чтобы оставшее количество спичек делился на 3.
и Петя выигрывает.
Вероятность того, что случайно взятый код содержит последовательность 123, равна отношению количества кодов, содержащих последовательность 123, к общему количеству кодов.
Так как коды составляются путем перестановок из десяти цифр, то их общее количество равно числу перестановок из 10:
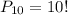
Так как нас интересует последовательность 123, то вместо цифр 1, 2, 3 будем сразу рассматривать эту последовательность. Итого имеем элементы: 0, 123, 4, 5, 6, 7, 8, 9. то есть всего 8 элементов. Общее количество кодов, которые можно получить, переставляя эти элементы, равно числу перестановок из 8:
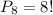
Таким образом, вероятность:
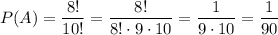
ответ: 1/90
Пусть сторона BC=x. Как известно, расстояние от вершины B треугольника ABC до точки D касания стороны BC с вписанной окружностью равно p-n=(10+x-n)/2. Как известно, расстояние от вершины C до точки E касания стороны BC с вневписанной окружностью также равно p-n. Возможны два случая.
1 случай. Точка D лежит между B и E. Тогда должно выполняться BD=DE=EC, откуда 3(p-n)=x; x=3n-30 (в частности, отсюда следует, что n>10). Выпишем еще три неравенства треугольника:
10+n>x; 10+x>n; n+x>10. Два последних дают x>|n-10|, а поскольку по доказанному n>10, имеем |n-10|=n-10, то есть x>n-10.
Подставим в неравенства 10+n>x и x>n-10 значение x=3n-30:
10+n>3n-30 и 3n-30>n-10; то есть
2n<40 и 2n>20; то есть 10<n<20, то есть n=11, 12, 13, 14, 15, 16, 17, 18, 19.
2 случай. Точка D лежит между E и C. Тогда BD/2=x/3; откуда x=30-3n, то есть n<10. Из неравенств треугольника в этом случае мы получаем
10+n>x и x>10-n. Подставляем в эти неравенства значение x=30-3n:
10+n>30-3n и 30-3n>10-n; 4n>20 и 2n<20; 5<n<10, то есть n=6, 7, 8, 9.
ответ: 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19.
Пошаговое объяснение: