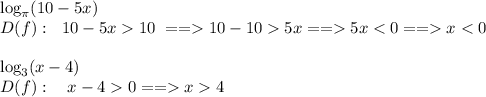Для начала давай разберемся с обозначениями в задаче.
- Знак ↑ означает возведение в степень.
- Знак ↓ означает падение в степень.
Теперь разберем пошаговое решение задачи.
Задача гласит: "А↑4 ↓n = 15 A↑3 ↓n - 2".
Давай посмотрим на левую часть уравнения "A↑4 ↓n". Это означает, что мы должны возвести число A в степень 4, а затем полученный результат нужно понизить до степени n.
Правая часть уравнения "15 A↑3 ↓n - 2" означает, что число A нужно возвести в степень 3, затем полученный результат нужно понизить до степени n, умножить на 15 и вычесть 2.
Теперь имея обе части уравнения, можем приступить к решению:
1. Распишем левую часть уравнения: A↑4 ↓n
Получаем: A * A * A * A / (n * n * n * n)
2. Распишем правую часть уравнения: 15 A↑3 ↓n - 2
Получаем: 15 * A * A * A / (n * n * n) - 2
3. Теперь соединим обе части уравнения и приравняем их друг другу:
A * A * A * A / (n * n * n * n) = 15 * A * A * A / (n * n * n) - 2
4. Чтобы упростить уравнение, умножим обе части на (n * n * n * n):
A * A * A * A = 15 * A * A * A * n - 2 * n * n * n * n
5. Поделим обе части на A * A * A:
A = 15 * n - 2 * n * n * n * n / (A * A * A)
6. Переставим выражение, чтобы избавиться от дробной части:
(A * A * A) = 15 * n * (A * A * A) - 2 * n * n * n * n
7. Теперь вынесем (A * A * A) за скобки:
1 = 15 * n - 2 * n * n * n * n / (A * A * A)
8. Выразим (A * A * A) в левой части уравнения:
(A * A * A) = 2 * n * n * n * n / (15 * n - 1)
Таким образом, мы получили уравнение, в котором выражено (A * A * A).
Если нам известны значения чисел A и n, мы можем подставить их в это уравнение и рассчитать значение (A * A * A).
Важно отметить, что для получения конкретного числового ответа, необходимо знать значения чисел A и n. Без этих данных, мы можем только выразить (A * A * A) через n.
Дано: В бидон налили 8 литров молока, и осталась незаполненной 1/3 часть бидона.
Мы должны найти количество литров, которое входит в бидон.
Для начала, давай определим, сколько литров молока осталось в бидоне.
Известно, что в бидоне осталась незаполненной 1/3 часть. Мы можем представить это в виде дроби: 1/3.
Чтобы найти количество молока, оставшегося в бидоне, нужно 8 литров умножить на эту дробь:
8 * 1/3 = 8/1 * 1/3 = 8/3 литров.
Теперь, чтобы определить, сколько литров входит в бидон, нужно от общей вместимости бидона (не учитывая остаток) отнять количество литров, которое осталось.
Вместимость бидона мы не знаем, но мы знаем, что осталось 8/3 литров, поэтому общая вместимость бидона должна быть больше этого значения.
Давай представим общую вместимость бидона в виде переменной x.
Тогда уравнение будет выглядеть так:
x - 8/3 = 0
Чтобы найти значение x, мы должны избавиться от 8/3 на левой части уравнения. Для этого умножим и разделим оба выражения на 8/3:
(x - 8/3) * (3/8) = 0 * (3/8)
После упрощения получаем:
3x/8 - 8/3 * 3/8 = 0
3x/8 - 24/24 = 0
3x/8 - 1 = 0
Теперь мы можем избавиться от -1 на левой части уравнения, прибавив 1 к обоим выражениям:
3x/8 - 1 + 1 = 0 + 1
3x/8 = 1
Чтобы избавиться от 3/8, мы можем умножить и разделить оба выражения на 3/8:
3x/8 * 8/3 = 1 * 8/3
3x = 8/3
Теперь нам нужно избавиться от 3 в знаменателе, умножив и разделив оба выражения на 3:
Відповідь:
1) x<0
2)x>4
Покрокове пояснення: