S(ABCD) = 13
Пошаговое объяснение:
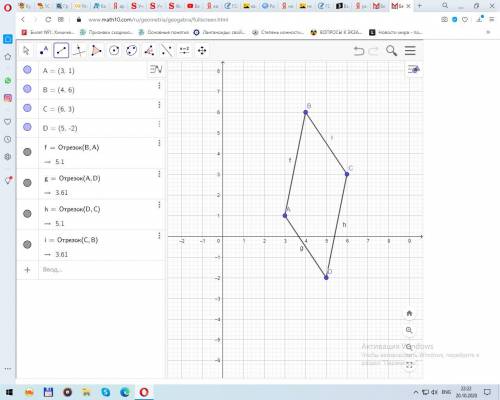
Определим вид четырехугольника.
Найдем длины его сторон:
AB = 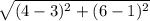 =
= 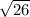
BC = 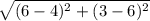 =
= 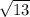
CD = 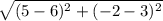 =
= 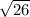
DA = 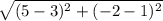 =
= 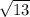
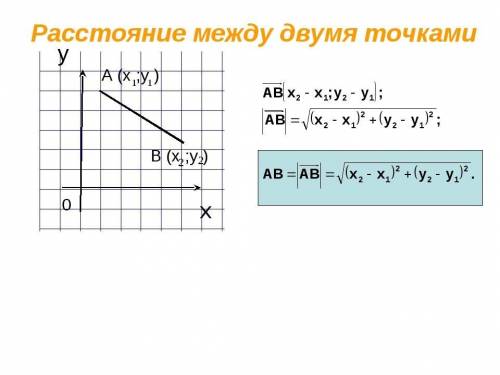
(используется формула расстояния между двумя точками)
У четырехугольника две пары равных сторон, значит, это параллелограмм(по признаку параллелограмма)
Для наглядности изобразим параллелограмм ABCD на координатной плоскости.
Площадь параллелограмма можно посчитать через сторону и высоту, проведенную к этой стороне:
S(ABCD) = h*a
Примем AB = a, тогда осталось найти высоту, проведенную к стороне AB. Эта высота равна расстоянию от точки C до прямой AB. Значит, можно посчитать высоту, используя формулу расстояния от точки до прямой.
Задаем уравнение прямой AB по двум точкам:
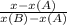 =
= 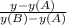
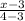 =
= 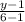
5x - 15 = y - 1
y = 5x - 14 - получили уравнение прямой AB
Запишем уравнение в виде Ax + By + C = 0
5x - y - 14 = 0 (то есть A = 5, B = -1, C = -14)
С(x₀; y₀) = C(6;3) , x₀ = 6, y₀ = 3
h = 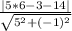 = 13/
= 13/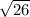
S(ABCD) = 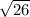 * (13/
* (13/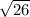 ) = 13
) = 13

Продукты Содержание витамина C,
мг/100 г продукта Продукты Содержание витамина C,
мг/100 г продукта
Морковь 5 Яблоки 10
Помидоры 25 Смородина чёрная 200
Картофель 20 Апельсин 60
Капуста цветная 50 Салат овощной 15
Пошаговое объяснение:
Задача на математический расчет.
Т. к. содержание витамина С дано в 100 г продукта, то нужно вычислять количество витамина С в зависимости от веса продукта, который указан в условии.
90 г цветной капусты → 45 мг витамина С, 110 г картофеля → 22 мг витамина С, 80 г помидоров → 20 мг витамина С и 1 апельсин массой 115 г → 69 мг витамина С.
Вычислим: 45 + 22 + 20 + 69 = 156. Округляем до целого 156.
Для того, чтобы исследовать функцию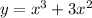 , найдем ее производную:
, найдем ее производную:
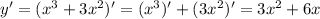
2).Приравняем производную к нулю и найдем абсциссы точек экстремума:
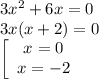
3).Исследуем знаки производной:
+++++++++++++++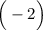 ---------------
---------------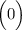 ++++++++++++++
++++++++++++++
Значит:
На промежутке![( - \infty; -2]](/tpl/images/1346/1524/a58e2.png) функция возрастает.
функция возрастает.
На промежутке![[-2;-1]](/tpl/images/1346/1524/6f3f7.png) функция убывает.
функция убывает.
На промежутке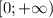 функция возрастает.
функция возрастает.
4).Найдем критические значения функции.
В точке максимума ( ):
):
В точке минимума: