Существует
Пошаговое объяснение:
На самом деле такое число найдётся для любой натуральной степени 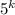 .
.
Я утверждаю, что для всех k найдётся число, состоящее из k цифр, не содержащее нулей в десятичной записи и делящееся на 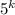 .
.
Доказываем по индукции.
База индукции. Для k = 1 подходит 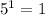 .
.
Индукционный переход. Пусть длина числа  равна k, десятичная запись этого числа не содержит нулей. Припишем к этому числу слева ненулевую цифру a и потребуем, чтобы получившееся число делилось на
равна k, десятичная запись этого числа не содержит нулей. Припишем к этому числу слева ненулевую цифру a и потребуем, чтобы получившееся число делилось на 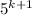 .
.
Получившееся число равно 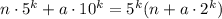 , оно будет делиться на
, оно будет делиться на 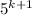 , если делится на 5.
, если делится на 5.
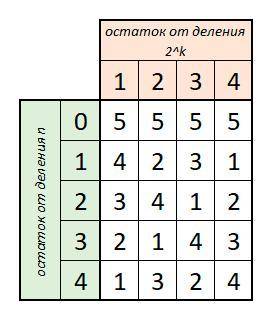
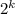 при делении на 5 может давать остатки 1, 2, 3 и 4; n может давать любые остатки от 0 до 4. Ниже в таблице я явно выписываю, какие можно взять a для каждой комбинации остатков. Например, если n даёт остаток 3 при делении на 5;
при делении на 5 может давать остатки 1, 2, 3 и 4; n может давать любые остатки от 0 до 4. Ниже в таблице я явно выписываю, какие можно взять a для каждой комбинации остатков. Например, если n даёт остаток 3 при делении на 5; 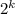 даёт остаток 4 при делении на 2, то можно взять a = 3: тогда
даёт остаток 4 при делении на 2, то можно взять a = 3: тогда 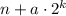 даёт такой же остаток при делении на 5, что и
даёт такой же остаток при делении на 5, что и 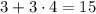 .
.
Таким образом, если для k такое число найдётся, то и для k + 1, а значит, и для всех k, в том числе и для k = 1987.
Вот, например, числа, построенные для k от 1 до 20:
5 25 125 3125 53125 453125 4453125 14453125 314453125 2314453125 22314453125 122314453125 4122314453125 44122314453125 444122314453125 4444122314453125 54444122314453125 254444122314453125 1254444122314453125 21254444122314453125Например, число 21254444122314453125 делится на 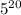 и не содержит нулей :)
и не содержит нулей :)
Наибольшее значение функции на промежутке [-1; 3] будет в точке x = 0, а наименьшее в точке x = 1,75
Пошаговое объяснение:
y = x^4 - 6 x^2 + 1
Найдём производную:
y' = 4 x^3 - 12 x + 0
y' = 4 x^3 - 12 x
y' = 4 x (x^2 - 3)
Найдём промежутки возрастания/убывания функции:
y' = 0
4 x (x^2 - 3) = 0
x^2 - 3 = 0 и x = 0
x^2 = 3
x1 = sqrt (3)
x2 = - sqrt (3)
Построив числовую ось получим, что функция возрастает на промежутках (-Б; - sqrt (3)) и (sqrt (3); +Б). А убывает на промежутке (- sqrt (3); sqrt (3)).
Значит, наибольшее значение функции на промежутке [-1; 3] будет в точке x = 0, а наименьшее в точке x = 1,75