В решении.
Пошаговое объяснение:
Как сделать:
тесьмой или верёвочкой, шнурком измерить длину окружности предмета; при линейки определить длину этой окружности в см; линейкой измерить диаметр указанного предмета. Потом первое число разделить на второе, занести все измерения и результаты вычислений в таблицу.
Длина окружности С Длина d С : d
Бокал 27 см 8,6 см ≈ 3,14
Крышка от крема 20,1 см 6,4 см ≈ 3,14
Тарелка 28,3 см 9 см ≈ 3,14
Задание. Найти производную функции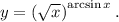 
Решение. Задана функция вида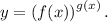 
Для нахождения производной данной функции выполняют следующие этапы:
1. Прологарифмировать обе части данного равенства по основанию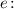 
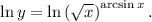
2. По свойству логарифмов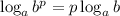 
имеем:
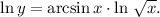
3. Найти производную двух частей равенства по переменной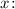 
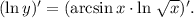
3.1. Используя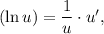 
имеем:
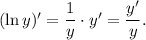
3.2. Используя правило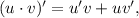 
имеем:
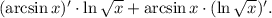
3.2.1. Используя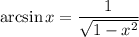 
и 
и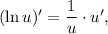меем:
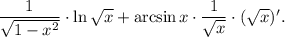
3.2.2. Используя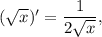 
имеем:
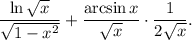
3.2.3. Упросим выражение и получаем:
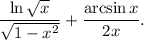
3.3. Имеем:
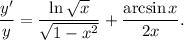
4. Умножим обе части равенства на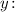 
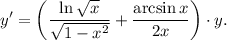
5. Поскольку из условия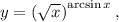 
то:
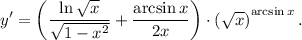
ответ: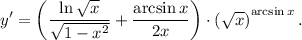
375] 21
(+- 1 сотая в ответах)