нужны краткие ответы Вопросы для подготовки к устному экзамену по математике за
2019-2020 учебный год
1. Комплексные числа и арифметические операции над ними. Возведение
комплексного числа в степень и решение квадратных уравнений.
2. Функция. Свойства функции (область определения; множество
значений функции; монотонность; четность (нечетность); ограниченность,
периодичность). Расскажите подробнее об одном из свойств
3. Основные элементарные функции, их свойства и графики. Расскажите
подробнее об одной из функций
4. Корни натуральной степени из числа и их свойства.
5. Степень с рациональным, иррациональным, действительным
показателем. Основные свойства.
6. Понятие логарифма числа. Основные свойства логарифмов.
7. Векторы в пространстве. Операции над ними. Скалярное произведение.
Действия с векторами, заданными координатами.
8. Понятия синуса, косинуса, тангенса и котангенса числа
9. Основные тригонометрические тождества, формулы двойного
аргумента, формулы сложения тригонометрических функций
10. Формулы приведения. Формулы сложения
11. Перечислить основные методы иррациональных уравнений и
неравенств. Показать применение одного из них
12. Перечислить основные методы решения показательных уравнений и
неравенств. Показать применение одного из них
13. Перечислить основные методы решения логарифмических уравнений и
неравенств. Показать применение одного из них
14. Перечислить основные методы решения тригонометрических
уравнений и неравенств. Показать применение одного из них
15. Взаимное расположение прямых в пространстве, прямой и плоскости.
Теорема о трех перпендикулярах.
16. Аксиомы стереометрии, два следствия из аксиом.
17. Сечения многогранников и тел вращения
18. Понятие о многогранниках, их виды (определение, площадь, объѐм ).
19. Тела вращения, их виды (определение, площадь, объѐм).
20. Числовая последовательность задания и свойства числовых
последовательностей. Предел последовательности.
21. Производная функции. Физический и геометрический смысл
производной. Правила дифференцирования. Производная второго порядка
22. Экстремумы функции. Алгоритм нахождения экстремумов функции.
23. Определение первообразной. Основное свойство первообразной. Три
правила нахождения первообразной.
24. Понятие определенного интеграла. Применение определенного
интеграла для нахождения площади криволинейной трапеции.
25. Основные понятия комбинаторики. Бином Ньютона. Треугольник
Паскаля
26. Вероятность события. Сложение и умножение вероятностей.
Классическое определение вероятности.
 +4.85-10
+4.85-10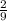 -17
-17 -3.85
-3.85 +
+ -
-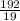 -
-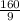 -
-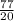
 =-33
=-33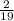
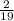
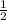 +5
+5 )=-5
)=-5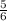
 +
+ )=-
)=-
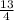 =-
=-
 +
+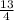

 =-2
=-2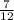 =-2.583
=-2.583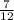 =-2.583
=-2.583
ответ:ёлялялялляляляляляял
Пошаговое объяснение мы стобою дрзья