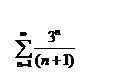
задача №1
Sпр=а*b
1) 12*36=432 (см2) - площадь всего прямоугольника
2) 432/27*1=16 (см2)
ответ: площадь 1/27 части прямоугольника равна 16 см2
задача №2
1) 12+3=15 (км/ч) - скорость второго велосипедиста
2) 12+15=27 (км/ч) - скорость сближения
3) 81:27=3 (ч)
ответ: велосипедисты встретятся через 3 часа
задача №3
если по 23 ученика в 3 классах
23*3= 69 (ст) нужно
если по 24 ученика в 3 классах
24*3= 72 (ст) нужно
ответ: если в каждом из трех классов по 23 ученика, то 70 стульев хватит. Если по 24 ученика в трех классах, то стульев не хватит.
задача №1
Sпр=а*b
1) 12*36=432 (см2) - площадь всего прямоугольника
2) 432/27*1=16 (см2)
ответ: площадь 1/27 части прямоугольника равна 16 см2
задача №2
1) 12+3=15 (км/ч) - скорость второго велосипедиста
2) 12+15=27 (км/ч) - скорость сближения
3) 81:27=3 (ч)
ответ: велосипедисты встретятся через 3 часа
задача №3
если по 23 ученика в 3 классах
23*3= 69 (ст) нужно
если по 24 ученика в 3 классах
24*3= 72 (ст) нужно
ответ: если в каждом из трех классов по 23 ученика, то 70 стульев хватит. Если по 24 ученика в трех классах, то стульев не хватит.
ответ: ряд расходится.
Пошаговое объяснение:
1) Составляем выражение для n+1 - го члена: a(n+1)=3^(n+1)/(n+2)=3*3^n/(n+2).
2) Составляем отношение n+1 - го члена к n - му: a(n+1)/a(n)=3*(n+1)/(n+2).
3) Находим предел этого отношения при n⇒∞: он равен 3>1, поэтому по признаку Даламбера ряд расходится.
Вообще говоря, здесь можно обойтись и без признака Даламбера. Так как при любом n 3^n>n+1, то a(n) при n⇒∞ не стремится к нулю, а это достаточный признак расходимости ряда.