Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
6=a·o+t ⇒ t=6; 0=a·4+t ⇒ a=-6/4=-1,5
y = -1,5x+6
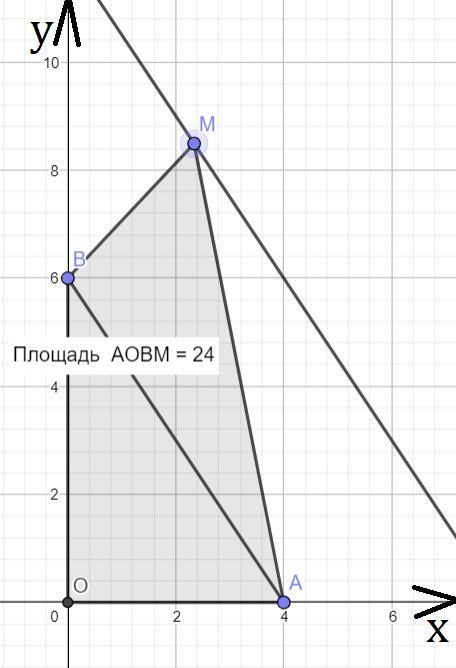
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-1,5x+6.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=24, S(AOB)=AO·OB/2=12.
Тогда S(BMA)=12.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -1,5
ответ: -1,5.
ответ
1 вопроса
{{x==0},{x==4}}
((4-x)*x^3)==0
0==(-4*x^3)+x^40==((-4+x)*x^3)
ответ
2 вопроса
{{x==-Rationalize(0.69444465211)},{x==-Rationalize(0.16900813027)},{x==Rationalize(0.07985118528)+I*-Rationalize(0.14327667443)},{x==Rationalize(0.07985118528)+I*Rationalize(0.14327667443)},{x==Rationalize(0.70375041181)}}
(-1)/x^2-(220*x)+(450*x^3)==0
0==1/x^2+(220*x)-(450*x^3)
0==(1+(220*x^3)-(450*x^5))/x^2
ответ
3 вопроса
{{x==1/(2*Sqrt(6))}}
Sqrt(x^4)==-1/24
ответ
4 вопроса
Sqrt(x^4)==-1/24
(2*Cos1/180)*Pi)*x)))+Tan1/180)*Pi)*x))==0
0==(4*Cos1/180)*Pi)*x)))+(2*Tan1/180)*Pi)*x)))
0==4*(1/(2*E^(((I/180)*Pi)*x))+E^(((I/180)*Pi)*x)/2)+I*2*(E^-I)/180)*Pi)*x)-E^(((I/180)*Pi)*x))/(E^(((-I/180)*Pi)*x)+E^(((I/180)*Pi)*x))
ответ
5 вопроса
{{x==(Surd(-5,3)*Surd((-1)^2,3))/Surd(2^2,3)},{x==-Surd(5,3)/Surd(2^2,3)},{x==(-Surd((-1)^2,3)*Surd(5,3))/Surd(2^2,3)}}
((-5)-(4*x^3))/x==0
0==5/x+(4*x^2)
0==(5+(4*x^3))/x
у=53, х=161, (х+у):2=107
Пошаговое объяснение:
закономерность выглядит таким образом:
а, в, с, а... - где в=а+2, с=3в
на отрезке 51, у, 159 у=в=51+2=53;
на отрезке 159, х, 483 х=в=159+2=161.
(х+у):2=(53+161):2=107