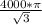Всего бочонков 90, из них надо найти вероятность, что на бочонке будет число от 1 до 45, таких бочонков 45 штук.
Пусть вытянули бочонок с номером от 1 до 45.
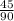 - вероятность того, что на первом вытянутом бочонке будет число от 1 до 45.
- вероятность того, что на первом вытянутом бочонке будет число от 1 до 45.
Но так как второй бочонок мы будем доставать из той же кучи, то после первого вытянутого бочонка в куче останется всего 89 бочонков, из которых 44 бочонка меньше 46 (события зависимые).
 - вероятность того, что на втором вытянутом бочонке будет число от 1 до 45.
- вероятность того, что на втором вытянутом бочонке будет число от 1 до 45.
Чтобы найти их общую вероятность, надо перемножить их вероятности:
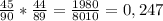
ответ: 0,247
1. Угол С = 180-125=55
Угол А равен углу С (треугольник равнобедренный по условию)
Угол А=55
Угол B = 180 - (угол С + угол А) (теорема о сумме углов треугольника
Угол B = 180-110=70
ответ: А=55; B=70; C=55
2. Угол D = 44 по свойству вертикальных углов
Угол К равен углу D по свойству равнобедренного треугольника
Угол K=44
Угол C = 180 - (угол D + угол K) по теореме о сумме углом треугольника
Угол С = 180-88=92
ответ: К=44; С=92; D=44
3. Угол М равен 32 по свойству вертикальных углов
Угол P равен углу Т по свойству равнобедренного треугольника
Угол Р = углу Т = (180-угол М):2 по теореме о сумме углов треугольника.
Угол P= угол Т = (180-32):2=74
а) 100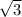 б)
б) 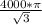
Пошаговое объяснение:
Т.к. осевое сечение является правильным треугольником, а радиус основания r равен 10, значит все стороны это треугольника равны 20. Опустим высоту из вершины этого треугольника и найдем ее длину по теореме Пифагора: h= =10
=10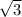 . Теперь найдем площадь треугольника, зная его высоту, а радиус основания конуса будет половиной основания этого треугольника: S=
. Теперь найдем площадь треугольника, зная его высоту, а радиус основания конуса будет половиной основания этого треугольника: S=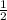 hr=
hr=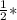 20*10
20*10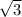 =100
=100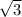
Объем конуса равен V=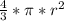 *h. Радиус основания r и высота конуса h нам уже известны. Подставляем значения: V=
*h. Радиус основания r и высота конуса h нам уже известны. Подставляем значения: V=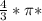 100*10
100*10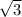 =
=