Имеется 10 палочек длины 1; 1,9 ; 1,9² ;;1,9⁹ . Можно ли из этих палочек, используя не обязательно все, сложить а) треугольник б) равнобедренный треугольник? МАКСИМАЛЬНО подробно .Актуально до 15.00 МСК, 17.06.20.
а) Можно. Для этого удобно брать палочки, идущие подряд. Возьмем первые 5 палочек: .
Построим треугольник ABC: . Заметим, что , поэтому можно не рассматривать неравенства треугольника, включающие эту сторону. Осталось доказать, что . Действительно по формуле суммы геометрической прогрессии. Но . Проверим истинность этого неравенства: .
б) Предположим, что можно. Тогда, в частности, можно составить два одинаковых отрезка. Рассмотрим набор степеней числа , которые формируют первый отрезок. Пусть это числа , для второго отрезка возьмем степени . Получим (*). Теперь становится ясно, почему это не может быть верно. Ведь то, что мы видим, похоже на запись числа в системе счисления, пусть и "необычной". Но двух различных записей одного числа не бывает. Однако трудно говорить об этом, имея дробную систему счисления. Пусть , другими словами, степени расставлены по порядку. Умножим уравнение на , получим только целые числа вида . Пусть . Выберем такое число , что . Тогда число записано в системе счисления 190, поскольку, как легко видеть, . Отсюда и следует наше противоречие.
Впрочем, кажется, что это перебор, и можно было решить проще: в (*) вычеркнем равные члены с обеих сторон. Получим, что сумма разных степеней равна другой сумме разных степеней. Теперь в левой части к большим степеням перекинем с правой стороны меньшие, а для правой части наоборот. Значит, отрицательное число равно положительному. Противоречие.
Однако для тренировки, мне представляется, было полезно рассмотреть оба подхода.
Начнем с формулировки признака делимости на 3: целое число делится на 3, если сумма его цифр делится на 3, если же сумма цифр данного числа не делится на 3, то и само число не делится на 3.
Из приведенной формулировки понятно, что признаком делимости на 3 не удастся воспользоваться без умения выполнять сложение натуральных чисел. Также для успешного применения признака делимости на 3 нужно знать, что из всех однозначных натуральных чисел на 3 делятся числа 3, 6 и 9, а числа 1, 2, 4, 5, 7 и 8 – не делятся на 3.
Теперь можно рассмотреть простейшие примеры применения признака делимости на 3. Выясним, делится ли на 3 число −42. Для этого вычисляем сумму цифр числа −42, она равна 4+2=6. Так как 6 делится на 3, то в силу признака делимости на 3 можно утверждать, что и число −42 делится на 3. А вот целое положительное число 71 на 3 не делится, так как сумма его цифр равна 7+1=8, а 8 не делится на 3.
А делится ли на 3 число 0? Чтобы ответить на этот вопрос, признак делимости на 3 не понадобится, здесь нужно вспомнить соответствующее свойство делимости, которое утверждает, что нуль делится на любое целое число. Таким образом, 0 делится на 3.
Натуральное число делится на 3 без остатка, если сумма его цифр кратна трем.
Число 762 делится на 3 без остатка, так как сумма его цифр: 7 + 6 + 2 = 15 — кратна 3 ( 15 : 3=5 ).
Число 4587 делится на 3 без остатка, так как сумма его цифр: 4 + 5 + 8 + 7 = 24 — кратна 3 ( 24 : 3=8 ).
Число 3572 не кратно 3, так как сумма его цифр: 3 + 5 + 7 + 2 = 17 — не делится на 3 без остатка ( 17 : 3=5 2 3 ).
Признак делимости на 9 такой же, как и на 3. Натуральное число делится на 9 без остатка, если сумма его цифр кратна девяти.
Число 765 делится на 9 без остатка, так как сумма его цифр: 7 + 6 + 5 = 18 — кратна 9 ( 18 : 9=2 ).
Число 4698 кратно 9, так как сумма его цифр: 4 + 6 + 9 + 8 = 27 — делится на 9 без остатка ( 27 : 9=3 ).
Число 3572 не кратно 9, так как сумма его цифр: 3 + 5 + 7 + 2 = 17 — не делится на 9 без остатка ( 17 : 9=1
Дзеянне твора адбываеца ў былой заходняй Беларусі, якая ў 1921 годзе была аддадзена пад уладу Польшчы. У пачатку аповесці Даніку было ўсяго сем гадоў. Ён па-дзіцячы глядзіць на свет і жыве сваімі дзіцячымі радасцямі і засмучэннямі. Крыўдна, а часам горка і балюча, калі цябе дражняць, асабліва жабраком. Іншы раз можна пацярпець, але найчасцей трэба не даваць сябе ў крыўду, адбівацца, а часам уцякаць плачучы і клікаць на дапамогу маці. Даніку вельмі хочацца ў школу. Яна вабіць хлопчыка новым незнаёмым светам, якім жывуць старэйшыя вучні, а яшчэ вельмі хочацца абуць новыя бліскучыя боцікі (першыя ў жыцці!), што мама купіла да школы. У канцы аповесці Даніку дванаццаць гадоў і сярод аднакласнікаў вылучаецца асаблівымі здольнасцямі да навукі. Ён не можа мірыцца з тым, што ў школе дзеці вучацца на чужой мове, што багатыя яго аднакласнікі насміхаюцца з беднасці. Вялікі ўплыў на Даніка аказалі ўмовы жыцця, а таксама дарослыя. Яму пашчасціла сустрэцца з цудоўнымі настаўнікамі: вясковым чалавекам Міколам Кужалевічам і польскай настаўніцай пані Мар'яй. Мікола Кужалевіч адкрыў Даніку сілу еднасці, братэрства працоўных, гаварыў пра нацыянальную годнасць беларусаў. Пані Мар'я абудзіла любоў і павагу да польскага народа, паказала Даніку працоўную Польшчу, багацце яе літаратуры і мовы. Прайшоў час — і ўжо сам Малец гуртаваў вакол сябе аднакласнікаў, дзяцей беднаты, каб усе трымаліся адзін аднаго. Але жыццё сутыкала героя і з іншымі настаўнікамі, такіх, як Цаба, Рузя, Дулемба. Хлопчык не мог назваць іх сваімі настаўнікамі, бо тыя ненавідзелі вучняў, абражалі іх, асабліва і пагардліва ставіліся да дзяцей беларусаў. І галоўны герой аповесці сам стаў вучыць сваіх равеснікаў чытаць на роднай мове. Хлопец многа думаў, аналізаваў убачанае і пачутае, шукаў адказы на пытанні, якія ставіла перад ім жыццё. Таму ў канцы аповесці Данік — не проста хлопчык, а сын свайго народа і ратавальнік сваёй роднай мовы
а) Можно. Для этого удобно брать палочки, идущие подряд. Возьмем первые 5 палочек: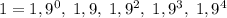 .
.
Построим треугольник ABC: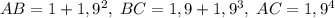 . Заметим, что
. Заметим, что 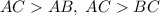 , поэтому можно не рассматривать неравенства треугольника, включающие эту сторону. Осталось доказать, что
, поэтому можно не рассматривать неравенства треугольника, включающие эту сторону. Осталось доказать, что 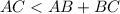 . Действительно
. Действительно 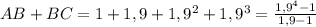 по формуле суммы геометрической прогрессии. Но
по формуле суммы геометрической прогрессии. Но 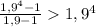 . Проверим истинность этого неравенства:
. Проверим истинность этого неравенства: 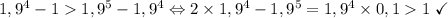 .
.
б) Предположим, что можно. Тогда, в частности, можно составить два одинаковых отрезка. Рассмотрим набор степеней числа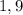 , которые формируют первый отрезок. Пусть это числа
, которые формируют первый отрезок. Пусть это числа 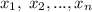 , для второго отрезка возьмем степени
, для второго отрезка возьмем степени 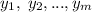 . Получим
. Получим 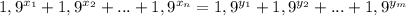 (*). Теперь становится ясно, почему это не может быть верно. Ведь то, что мы видим, похоже на запись числа в системе счисления, пусть и "необычной". Но двух различных записей одного числа не бывает. Однако трудно говорить об этом, имея дробную систему счисления. Пусть
(*). Теперь становится ясно, почему это не может быть верно. Ведь то, что мы видим, похоже на запись числа в системе счисления, пусть и "необычной". Но двух различных записей одного числа не бывает. Однако трудно говорить об этом, имея дробную систему счисления. Пусть 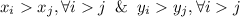 , другими словами, степени расставлены по порядку. Умножим уравнение на
, другими словами, степени расставлены по порядку. Умножим уравнение на 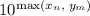 , получим только целые числа вида
, получим только целые числа вида 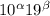 . Пусть
. Пусть 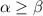 . Выберем такое число
. Выберем такое число 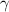 , что
, что 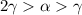 . Тогда число
. Тогда число 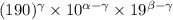 записано в системе счисления 190, поскольку, как легко видеть,
записано в системе счисления 190, поскольку, как легко видеть, 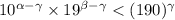 . Отсюда и следует наше противоречие.
. Отсюда и следует наше противоречие.
Впрочем, кажется, что это перебор, и можно было решить проще: в (*) вычеркнем равные члены с обеих сторон. Получим, что сумма разных степеней равна другой сумме разных степеней. Теперь в левой части к большим степеням перекинем с правой стороны меньшие, а для правой части наоборот. Значит, отрицательное число равно положительному. Противоречие.
Однако для тренировки, мне представляется, было полезно рассмотреть оба подхода.