Question

. В каком количестве точек достаточно проверить совпадение значений двух многочленов четвертой степени, чтобы доказать их тождественное равенство?​

Answer 1

Докажем, что пяти достаточно.

Пусть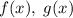 $f(x),\; g(x)$ два многочлена четвертой степени, которые совпадают в пяти точках. Тогда $f(x)-g(x)$ является многочленом, имеющим пять корней. Но степень многочлена

Четырех может быть недостаточно: Всего у многочлена четвертой степени пять коэффициентов, значит, пять неизвестных. Четыре уравнения не всегда дают единственное решение.

Можно доказать и более общий результат:

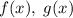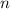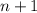Если $f(x),\; g(x)$ — многочлены, степени $n$, то $n+1$ — минимальное количество точек, в которых достаточно проверить совпадение многочленов, чтобы доказать их тождественное равенство.

База: для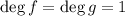 $\deg f=\deg g=1$ все очевидно: по аксиоме требуется две точки для однозначного определения прямой.

Переход: пусть для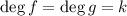 $\deg f=\deg g=k$ верно. Докажем истинность для 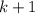$k+1$. Для этого предположим обратное: достаточно 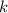$k$ точек. Возьмем различные многочлены 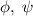$\phi,\; \psi$ степени