А1.
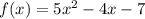
Найдём производную данной функции.

Найдём нули производной.
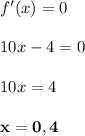
Определим знак производной на каждом промежутке.
- + 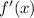
---------------------------------- ----------------------------------> x
----------------------------------> x
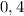
Функция возрастает там, где её производная положительна. А значит, она возрастает на промежутке 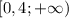 . Из перечня ответов полностью в этот промежуток входит только
. Из перечня ответов полностью в этот промежуток входит только  .
.
ответ: 3.
А2.
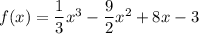
Найдём производную данной функции.
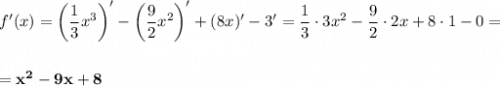
Найдём нули производной.
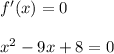
По теореме Виета:

Определим знак производной на каждом промежутке.
+ - + 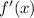
-------------------- -----------------------
----------------------- --------------------> x
--------------------> x

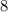
Функция убывает там, где её производная отрицательна. В нашем случае, на промежутке ![\bf{[1; 8]](/tpl/images/1729/3052/46b37.png) . Ему соответствует вариант номер 2.
. Ему соответствует вариант номер 2.
ответ: 2.
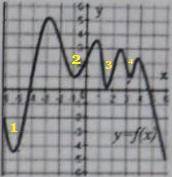
А3.
В точках минимума функция из убывания переходит в возрастание. На данном графике 4 такие точки (см. вложение).
ответ: 1.
А4.
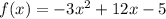
Найдём производную данной функции.
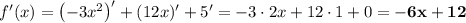
Найдём нули производной.
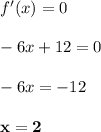
Точки максимума соответствуют точкам смены знака производной с плюса на минус. Проверим это, определив её знак на каждом промежутке:
+ - 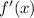
---------------------------------- ----------------------------------> x
----------------------------------> x
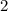
Полученные знаки соответствуют изложенному выше условию. Значит, 2 является точкой максимума функции.
ответ: 4.
А5.
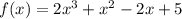
Найдём производную.
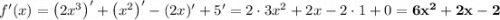
Найдём нули производной.

У производной нашлось 2 нуля. В то же время, производная равна нулю в точках экстремума графика функции. А значит, функция имеет две точки экстремума.
ответ: 1.
А6.
Точки максимума на графике производной соответствуют точкам смены знака производной с плюса на минус. На нашем графике это происходит в точке с абсциссой 3.
ответ: 2.
А7.
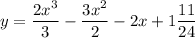
Найдём производную функции.
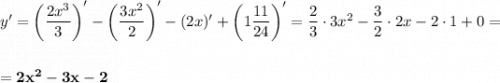
Найдём нули производной.
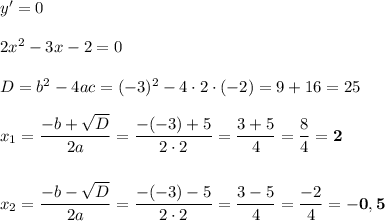
У производной нашлось 2 нуля. Найдём её знак на каждом промежутке.
+ - + 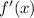
------------------ -------------------
------------------- -------------------> x
-------------------> x
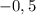
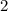
Точки минимума соответствуют точкам смены знака производной с минуса на плюс. Такой точке соответствует 2.
ответ: 4.
А8.
На заданном отрезке функция имеет одну точку максимума. Она соответствует значению функции, равному трём.
ответ: 2.
Пошаговое объяснение:
ДОБАВИТЬ СВОЙ ОТВЕТ
Задание
А Б В Г
0,5 5 50 1
2. Знайдіть число, 1% якого дорівнює 11.
А Б В Г
1,1 11 110 1100
3. Знайдіть 11% від числа 200.
А Б В Г
22 2,2 11 220
4. Знайдіть число, 12% якого дорівнює 60.
А Б В Г
50 500 7,2 5
5. Установіть відповідність між задачами (1-4) та їх значеннями (А-Д):
1 5% від 12,4 А 0,62
2 120% від 3,5 Б 191
3 95,5% від 200 В 1,659
4 15,8% від 10,5 Г 4,2
Д 16,59
А Б В Г Д
1
2
3
4
6. Установіть відповідність між квадратами (1-4) та площею зафарбованих фігур, яку подано у відсотках від загальної площі (А-Д).
А 75%
Б 40%
В 25%
Г 20%
Д 50%
А Б В Г Д
1
2
3
4
7. 30% градусної міри кута АОВ дорівнюють 30 гр. Знайдіть градусну міру кута АОВ.
8. У шкільному саду ростуть 40 фруктових дерев, 30% із них – яблуні. Скільки яблунь росте у шкільному саду?
9. Ділянка поля має форму прямокутника зі сторонами 30 м і 150 м. 35% площі всього поля засіяли пшеницею. Яка площа частини поля, що займає пшениця?
10. Знайдіть 15% від кореня рівняння 2,8х – 3,1х + 4,5х = 84.
11. Туристи за перший день подорожі проїхали 30%, другого дня – 25% усього шляху, а третього 90 км. Яка довжина всього шляху?
12. 12 грамів 9%-го розчину солі випарили до 8 г. Яким є відсоток отриманого розчину
6 мм
Объяснение:
Средняя линия треугольника равна половине основания, поэтому ВС=2КО=6√2 мм.
АВ=ВС=6√2 мм по условию
ВК=АК=6√2/2=3√2 мм
ΔКОВ - прямоугольный, равнобедренный
По теореме Пифагора ВО²=КО²+КВ²=(3√2)²+(3√2)²=36; ВО=√36=6 мм.