Question

Найдите промежутки убывания функции

Answer 1

у=х³+15х²-36х+1

у=2х²+225х-36

2х²+225х-36=0

D=50337, х₁=-(225+-корен 50337)/4, х₂=(225+-корен 50337)/4 наверное так

Пошаговое объяснение:

Answer 2

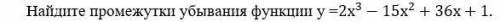
1) Найдём производную данной функции

$y^` = 6x^2-30x+36$

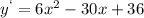
2) Приравняем её к нулю и сократим на 6

$x^2-5x+6=0$

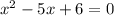
3) Найдём корни этого уравнения по т. Виета

$x_1x_2=6\\x_1+x_2= 5$

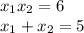
Нам подходят

$x1=3\\x2=2$

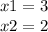
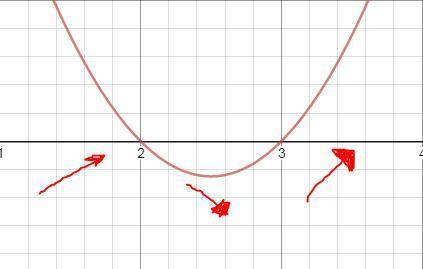
4) Расположим их на числовой прямой. График производной 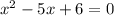$x^2-5x+6=0$ задаёт параболу, ветви которой направлены вверх. в точках 2 и 3 парабола пересекает числовую прямую. ОБРАТИТЕ ВНИМАНИЕ - НА РИСУНКЕ ПРЕДСТАВЛЕН ГРАФИК ПРОИЗВОДНОЙ

5) По графику видно, то при x≤2 и x≥3 производная положительная, т.е, исходная функция возрастает.

6) В промежутке x ∈ [2;3] производная отрицательная, т.е исходная функция убывает

ответ: [2;3]