≈0,36
Пошаговое объяснение:
Количество благоприятных исходов: С₅²=10
Всего вариантов: С₈²=28
Р= С₅²/С₈²
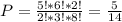 ≈0,36
≈0,36
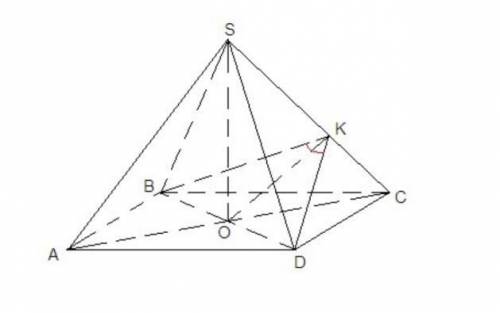
Из задания выходит, что задана правильная четырёхугольная пирамида SАВСД, высота SO которой равна ребру "a". Точка О - центр основания (точка пересечения его диагоналей).
Пусть длина ребра основания а = 1, диагональ основания d = √2.
Для определения угла между смежными боковыми гранями проведём сечение через диагональ ВД основания перпендикулярно боковому ребру . Получим равнобедренный треугольник ВКД, угол К которого равен углу между боковыми гранями.
Высоту из вершины К этого треугольника найдём как высоту h из вершины прямого угла в треугольнике SOД. Для этого найдём длину бокового ребра SД:
SД = √(1² + (√2/2)²) = √(1 + (2/4)) = √(3/2).
h = (1*(√2/2)/√(3/2) = 1/√3.
Теперь можно получить ответ:
угол ВКД = 2arc tg((d/2)/h) = 2arc tg((√2/2)/(1/√3)) = 2arc tg√(3/2) =
= 2*50,76848 = 101,537 градуса.
Вероятность того, что обе детали оказались окрашенными —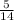 .
.
Пошаговое объяснение:
Вынимание первой детали:
Когда мы вынимаем первую деталь, в коробке у нас 5 окрашенных деталей из 8. Соответственно, вероятность вынуть окрашенную деталь —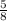 , так как:
, так как:
Вероятность = число благоприятных исходов : число всех исходов
Что в итоге:
Если же мы вынули окрашенную деталь, то мы продолжаем вынимать, а в коробке осталось:
1) 8 - 1 = 7 ( д. ) — всего.
2) 5 - 1 = 4 ( д. ) — окрашенных.
Если же нет — то вынимать далее бессмысленно, так как надо, чтобы обе детали были окрашенными, а одна из них не окрашена.
Вынимание второй детали:
Когда мы вынимаем вторую деталь — вероятность того, что мы вынем окрашенную деталь равна , так как в коробке осталось уже 7 деталей, из них 4 — окрашены.
, так как в коробке осталось уже 7 деталей, из них 4 — окрашены.
Рассчитаем вероятность:
Значит, вероятность вынуть 2 окрашенные детали равна:
3)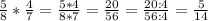 - вероятность того, что обе детали оказались окрашенными.
- вероятность того, что обе детали оказались окрашенными.
Здесь мы воспользовались правилом, которое гласит (я его переформулировал):
Вероятность происхождения двух событий равна вероятности происхождения первого события умноженной на вероятность происхождения второго события.