Дан интервал (−14;4).
а) числовое множество, содержащееся в этом интервале:
2) [−12;3]
б) числовое множество, не содержащееся в этом интервале:
3) [4;10]
в) целое число, принадлежащее данному интервалу и отстоящее на одинаковое расстояние от его концов (запиши число): -5
Пошаговое объяснение:
а) -14<-12, а 3<4, поэтому числовое множество [−12;3] принадлежит интервалу: (−14;4)
б) 10>4, поэтому числовое множество [4;10] не принадлежит интервалу (−14;4)
в) длина интервала (−14;4) равна 14+4, то есть 18.
18:2 = 9
4-9 = -5 (или -14+9 = -5)
Таким образом, целое число, принадлежащее данному интервалу и отстоящее на одинаковое расстояние от его концов равно -5.
84.
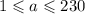
Правильная дробь имеет вид:
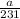
230 правильных дробей.
Из этого числа нужно исключить
сократимые дроби.
Все делители числа 231:
1; 3; 7; 11; 21; 33; 77; 231.
Числители, кратные 3
(только для правильных дро
бей):
3n ---- 7×11-1=77-1=76
Числители, кратные 7:
7n ---- 3×11-1=33-1=32
Числители, кратные 11:
11n ---- 3×7-1=21-1=20
Числители, кратные 21:
21n ----- 11-1=10
Числители, кратные 33:
33n ----- 7-1=6
Числители, кратные 77:
77n ----- 3-1=2
76+32+20+10+6+2=146 правиль
ных сократимых дробей.
230-146=84 несократимых пра
вильных дробей.
84.

5,33 см³.
Пошаговое объяснение:
Объем правильной четырехугольной пирамиды:
V = 1/3 * h * S(основания)
Найдём диагональ основания (по т. Пифагора):
1/2 диагонали основания равна: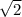 (см)
(см)
Найдём высоту пирамиды (по т. Пифагора):
Найдём площадь основания:
S(основания) = 2 * 2 = 4 (см²)
Найдём объём пирамиды:
V = 1/3 * 4 * 4 ≈ 5,33 (см³)