т.к в 1 четверти то косинус положителен.
sin²x+cos²x=1
cos²x=1-(8/17)²
cos²x=1-64/289
cos²x=225/289
cosx=√(225/289)
cosx=15/17
120
Пошаговое объяснение:
Пусть Саша выбрал число a, Андрей - число b, Оля - число c. Опишем последовательность действий.
1) Саша умножил своё число на каждое из других, получилось ab и ac. Затем вычел меньшее из большего. Тогда получается выражение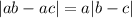 
. a можно вынести за модуль, так как оно натуральное.
2) Аналогично, у Андрея получилось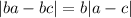 
.
У Оли получилось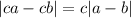 
3) По условию,
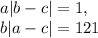
Из первого равенства можно получить два варианта:
а)
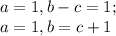
б)
,
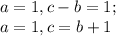поскольку 1 можно разложить на натуральные множители лишь
Рассмотрим второе равенство и подставим туда каждый случай из первого:
а)
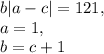
Отсюда:
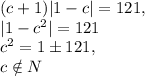
б)
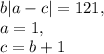
Отсюда:
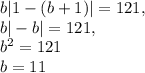
Далее находим c: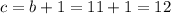 
Однозначно определяем число Оли: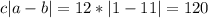 
120
Пошаговое объяснение:
Пусть Саша выбрал число a, Андрей - число b, Оля - число c. Опишем последовательность действий.
1) Саша умножил своё число на каждое из других, получилось ab и ac. Затем вычел меньшее из большего. Тогда получается выражение 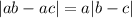. a можно вынести за модуль, так как оно натуральное.
2) Аналогично, у Андрея получилось .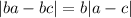
У Оли получилось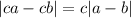
3) По условию,
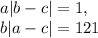
Из первого равенства можно получить два варианта:
а)
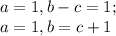
б)
,
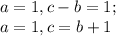поскольку 1 можно разложить на натуральные множители лишь
Рассмотрим второе равенство и подставим туда каждый случай из первого:
а)
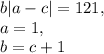
Отсюда:
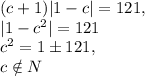
б)
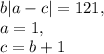
Отсюда:
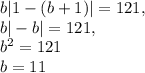
Далее находим c: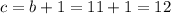
Однозначно определяем число Оли: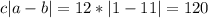
15/17
Пошаговое объяснение:
из основного тригонометрического тождества квадрат косинуса равен
1- 8*8/(17*17)=225/289
Синус равен 15/17 или -15/17. Но если угол в первой четверти, то синус положителен