Для решения подобных задач часто используют формулу Ньютона-Лейбница:
Да, мы здесь считаем интеграл для функции (как результат приравнивания и ). При этом, и .
Таким образом, искомая площадь равна (ед²).
Но можно было и заметить (смотрите рисунок ниже), что у нас получилась трапеция ("обычная", не "криволинейная"), площадь которой равна ( {площадь четырехугольника} + {площадь треугольника} ).
Жил-был Квадрат. В его стране все было квадратным: дома, клумбы, часы. Даже блинчики, которые пекла его мама, были квадратными.Все друзья и соседи были одинаковые. Однажды Квадрат спросил у своей мамы: "Почему мы никогда не ходим в соседний город?"- "Там живут другие фигуры, они не такие, как мы!" - ответила мама.Квадрату стало очень любопытно. Неужели есть другие фигуры? Решил он отправиться в путешествие. И вот, Квадрат вошел в соседний город. И вдруг, он увидел, как прямо на него несется что-то непонятное. Квадрат зажмурил глаза.- "Привет, ты кто?" - вдруг услышал он. Он открыл глаза и увидел мальчика, у которого совсем не было углов.- "Я квадрат. Я из соседнего города. А ты кто?"- "А я - Круг".- "Как ты можешь двигаться так быстро?"- "Это я на велосипеде. Машина ездит еще быстрее!"- "А у нас нет ни машин, ни велосипедов".- "Конечно, ведь квадратные колеса не могут крутиться".
Для решения подобных задач часто используют формулу Ньютона-Лейбница:
Да, мы здесь считаем интеграл для функции (как результат приравнивания
(как результат приравнивания  и
и 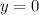 ). При этом,
). При этом, 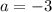 и
и 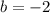 .
.
Таким образом, искомая площадь равна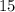 (ед²).
(ед²).
Но можно было и заметить (смотрите рисунок ниже), что у нас получилась трапеция ("обычная", не "криволинейная"), площадь которой равна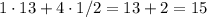 ( {площадь четырехугольника} + {площадь треугольника} ).
( {площадь четырехугольника} + {площадь треугольника} ).
ответ : 15 .