Ученик задумал натуральное число, не превышающее 50. Какова вероятность того, что это число а) Нечетное; Б) Делится на 5; с) Делится на 7; d) Больше 70.

👇

Увидеть ответ

Ответ:

Chumaeva79

29.08.2020

Пошаговое объяснение:

а) так как среди 50 натуральных чисел 25 - нечётных и 25 - чётных, то p=25/50=0,5;

b) Из 50 первых натуральных чисел на 5 делится 10 чисел, поэтому p=10/50=0,2;

с) На 7 делится 7 чисел, поэтому p=7/50=0,14;

d) так как по условию число не превышает 50, то p=0.

4,4(83 оценок)

Ответ:

VladeslavPavlo

29.08.2020

Пошаговое объяснение:

А) 50÷2=25

25—нечётных,то : 25/50=½=0,5

Б) На 5 делятся:5,10,15,20,25,30,35,40,45,50.

10 чисел, значит: 10/50=1/5=0,2

В)На 7 делятся: 7,14,21,28,35,42,49.

7 чисел, значит: 7/50=0,14

Д) невозможно, вероятность=0

4,7(39 оценок)

Открыть все ответы

Ответ:

queenames

29.08.2020

А) 37/48 : 5 2/7 - 19/42 * 7/8 + 4 1/5 = 37/48 : 37/7 - 19/48 + 4 1/5 = 37/48 * 7/37 -19/48 + 21/5 = 7/48 - 19/48 + 21/5 = - 12/48 + 21/5 = - 1/4 + 21/5 = - 5/20 + 84/20 = 79/20 =
= 3 19/20
б) (3 * 2/9 - 4* 1/1) : (10/3 - 3) = (2/3 - 1/3) : (10/3 - 9/3) = 1/3 : 1/3 = 1/3 * 3/1 = 1
в) 6 2/5 : 8/125 - 11 1/9 : 1 1/9 + 3 1/7 = 32/5 * 125/8 - 100/9 : 10/9 + 3 1/7 = 100 - 100/9 * 9/10 + 3 1/7 = 100 - 10 + 3 1/7 = 93 1/7
г) (3/5 * 1 7/11) - 1 7/11 : 10 = 3/5 * 1 7/11 - 1 7/11 : 10/1 = 3/5 *1 7/11 -1 7/11 * 1/10 =
1 7/11 * (3/5 - 1/10) = 1 7/11 * (6/10 - 1/10) = 18/11 * 5/10 = 9/11

4,8(70 оценок)

Ответ:

faceface96

29.08.2020

Для начало обозначим вершины треугольника как A,B,C

.
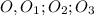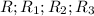Обозначим центр большей и меньших треугольников соответственно $O,O_{1};O_{2};O_{3}$ . так же радиусы $R;R_{1};R_{2};R_{3}$ .
Опустим три радиуса из вписанной окружности на все стороны , как известно радиус перпендикулярен касательной.
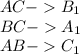Обозначим проекций радиуса на сторону $AC- B_{1}\\
BC- A_{1}\\ 
 AB-C_{1}$ .
Из этого следует что отрезки
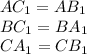
$AC_{1}=AB_{1}\\
BC_{1}=BA_{1}\\
CA_{1}=CB_{1}
$
Потому что отрезки касательных проведенные к окружности с одной точки равны .
Проведем биссектрисы из каждой вершины , они будут пересекаться в одной точке и это точка

.
Обозначим проекций маленьких окружностей на стороны J,T,N

.
Тогда очевидно мы получим трапецию у которой основания есть радиусы соответственных окружностей, всего трапеций 3.
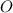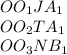То есть трапеций $OO_{1}JA_{1}\\
OO_{2}TA_{1}\\
OO_{3}NB_{1}$ .
Из каждой трапеций можно выразит по тереме Пифагора боковую сторону прямоугольной трапеций .
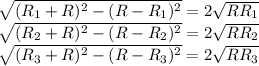
Они будут равны $\sqrt{(R_{1}+R)^2-(R-R_{1})^2}=2\sqrt{RR_{1}}\\
\sqrt{(R_{2}+R)^2-(R-R_{2})^2}=2\sqrt{RR_{2}}\\
\sqrt{(R_{3}+R)^2-(R-R_{3})^2}=2\sqrt{RR_{3}}\\$
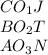Заметим так же что треугольники $CO_{1}J\\
BO_{2}T\\
AO_{3}N
$ будут подобны , большим прямоугольным треугольникам . Откуда из подобия получим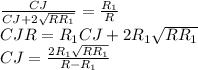
$\frac{CJ}{CJ+2\sqrt{RR_{1}}}=\frac{R_{1}}{R}\\
 CJR=R_{1}CJ+2R_{1}\sqrt{RR_{1}}\\
CJ=\frac{2R_{1}\sqrt{RR_{1}}}{R-R_{1}}$
И так все стороны. Достаточно найти эти три отрезка и просуммировать , так как отрезки касательных равны. В итоге получим
$BC=2\sqrt{RR_{1}}+\frac{2R_{1}\sqrt{RR_{1}}}{R-R_{1}}+2\sqrt{RR_{2}}+\frac{2R_{2}*\sqrt{RR_{2}}}{R-R_{2}}$
$AC=2\sqrt{RR_{1}}+\frac{2R_{1}\sqrt{RR_{1}}}{R-R_{1}} + 2\sqrt{RR_{3}}+\frac{2R_{3}\sqrt{RR_{3}}}{R-R_{3}}$
$AB=2\sqrt{RR_{2}}+\frac{2R_{2}\sqrt{RR_{2}}}{R-R_{2}} + 2\sqrt{RR_{3}}+\frac{2R_{3}\sqrt{RR_{3}}}{R-R_{3}}$
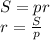
Теперь зная стороны , по формуле $S=pr\\r=\frac{S}{p}$
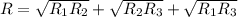
Я там все упростил и доделал , весьма сложные преобразований вышло но в итоге ответ такой вышел $R=\sqrt{R_{1}R_{2}}+\sqrt{R_{2}R_{3}}+\sqrt{R_{1}R_{3}}$