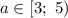ПЕРВЫЙ ВАРИАНТ РЕШЕНИЯ
Пусть х км/час – скорость второго легкового автомобиля.
За 7 часов первый автомобиль проехал:
S (расстояние) =v (скорость)*t (время)=110*7=770 км
Второй автомобиль за 7 часов проехал 7х км
Составим уравнение:
770+7х=1400
7х=1400-770
7х=630
х=90 км/час – скорость второго автомобиля.
ответ: скорость второго автомобиля составляет 90 км/ч.
ВТОРОЙ ВАРИАНТ
Рассмотрим две функции:
Изобразим данные функции на координатной плоскости.
Чтобы построить график функции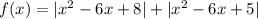 , следует раскрыть модуль на участках.
, следует раскрыть модуль на участках.
Найдем нули модулей функции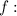
Рассмотрим функцию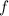 на пяти участках и раскроем модули в соответствии с участком (см. таблицу), используя правило:
на пяти участках и раскроем модули в соответствии с участком (см. таблицу), используя правило:
Построим график функции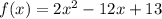 на участке
на участке 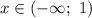 (см. пункт
(см. пункт 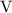 )
)
Построим график функции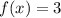 на участке
на участке ![x \in[1; \ 2]](/tpl/images/1356/5780/1fbb1.png)
Пересечение с осями координат:
1) с осью абсцисс: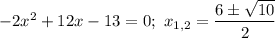
2) с осью ординат: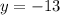
Построим график функции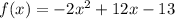 на участке
на участке ![x \in[1; \ 2]](/tpl/images/1356/5780/1fbb1.png)
Построим график функции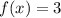 на участке
на участке ![x \in[4; \ 5]](/tpl/images/1356/5780/b98d5.png)
Построим график функции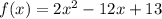 на участке
на участке 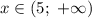
Пересечение с осями координат:
1) с осью абсцисс: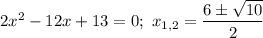
2) с осью ординат: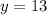
Изобразим график функции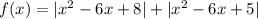 (см. рисунок).
(см. рисунок).
Уравнение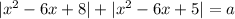 будет иметь более трех решений, если прямая
будет иметь более трех решений, если прямая 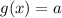 будет иметь более трех точек пересечения с графиком функции
будет иметь более трех точек пересечения с графиком функции 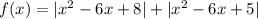
Изобразим возможные варианты решений (см. рисунок).
1) Если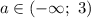 , то уравнение не имеет решений.
, то уравнение не имеет решений.
2) Если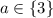 , то уравнение имеет множество решений (промежуток решений).
, то уравнение имеет множество решений (промежуток решений).
3) Если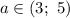 , то уравнение имеет 4 решения.
, то уравнение имеет 4 решения.
4) Если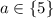 , то уравнение имеет 3 решения.
, то уравнение имеет 3 решения.
5) Если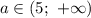 , то уравнение имеет 2 решения.
, то уравнение имеет 2 решения.
Таким образом, при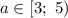 уравнение
уравнение 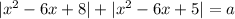 имеет более трех решений.
имеет более трех решений.
ответ: