Question

60. При каких значениях параметра m функция y = (m+2)x*2 + (m+2)х +m – 2 положительна
Для любых действительных значений х
с объяснением.​

Answer 1

$y=(m+2)x^2+(m+2)x+m-2\ \ \ ,\ \ \ y0\ ,\\\\1)\ \ m+2=0\ \ ,\ \ m=-2\\\\y=(-2+2)x^2+(-2+2)x-2-2=-40\ \ \Rightarrow \ \ \left\{\begin{array}{l}m+20\ ,\\D-2\ ,\\D=(m+2)^2-4(m+2)(m-2)-2\\-3m^2+4m+20-2\\-(m+2)(m-\frac{10}{3})$

$znaki:\ ---(-2)+++(\frac{10}{3})---\ \ \ \left\{\begin{array}{l}m-2\\m\in (-\infty;-2)\cup (\frac{10}{3};+\infty )\end{array}\right\\\\\\m\in (\dfrac{10}{3};+\infty )\ \ \ \Rightarrow \ \ \ \ m3\dfrac{1}{3}$

Answer 2

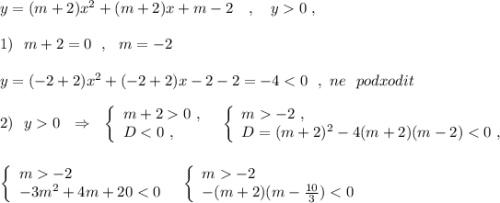
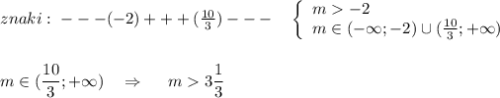
(m+2) x²+(m+2)*x+m-2<0

1) Если m=-2, то у=-4

2) Если m≠-2, получаем квадратичную функцию относительно х. Если первый коэффициент этой функции больше нуля, а дискриминант меньше нуля, то функция положительна при любом действительном значении х. Графически это означает, что парабола направлена ветвями вверх и не пересекается с осью ох.

m+2>0 ⇒m>-2, т.е. m∈(-2;+∞)

D(x)=(m+2)²-4(m²-4)<0 (D(x) -дискриминант относительно переменной х); m²+4m+4-4m²+16<0; -3m²+4m+20<0; 3m²-4m-20=0;

m=(2±√(4-60))/3=(2±8)/3; m=10/3; m=-2; решим неравенство

-3*(m-(10/3))(m+2)<0  методом интервалов.

-210/3

-                     +                             -

m∈(-∞;-2)∪(10/3;+∞)

С учетом m∈(-2;+∞) выходим на ответ А) m>10/3

m>3 1/3