Раз некоторое число удовлетворяет уравнению при любом , то оно также удовлетворяет уравнению при .
То есть, если мы подставим в уравнение , то выполнится равенство:
Оба корня удовлетворяют уравнению и ОДЗ (при ): с обеих сторон в первом случае получается , а во втором (так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
Очевидно, что эти два корня в ответ так сразу не пойдут. Мы знаем лишь только, что они подходят при . И если ответ на задачу существует, то он может быть только , или и , и . Но про другие значения мы пока ничего не знаем.
Посмотрим, что у нас будет получаться при :
Вот только первый логарифм не всегда существует. может быть отрицательным (возьмите, к примеру, ). А подлогарифмическое выражение обязано быть положительным. Значит, такой нас не устраивает.
Теперь проверим :
В обеих частях мы получили (так как , если ). Также , поэтому все ограничения будут выполняться.
Каждый из нас видит своим другом хорошего человека. Каким же я вижу настоящего друга? Прежде всего он должен быть доброжелательным, приветливым, отзывчивым — ведь людям так необходимы добро, бескорыстие, внимание. Настоящий друг должен быть хозяином своего слова, иметь современные взгляды на жизнь, уметь отстаивать свою точку зрения. Еще я хочу, чтобы человек, с которым я дружу, умел вести себя в обществе и всегда оставался самим собой. Я хочу, чтобы он уважал человеческую личность, а потому всегда был снисходительным, мягким и уступчивым. Качеств, которыми должен обладать настоящий друг, очень много, но прежде всего он должен быть действительно настоящим, а не поддельным. Настоящий друг тот — который придет на всегда. Народная мудрость гласит: «Не имей сто рублей, а имей сто друзей». И это так точно сказано! Ведь человек, не имеющий друзей, как нищий. Материал с сайта http://iEssay.ru Г. Державин отметил, что дружба не услуга, за нее не благодарят. Это верно, ведь друг, если он настоящий, никогда не потребует «платы» за свою дружбу. А настоящий друг — он не на день, не на месяц, очень часто люди проносят свою дружбу через всю жизнь.
Раз некоторое число
удовлетворяет уравнению при любом 
, то оно также удовлетворяет уравнению при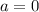 
.
То есть, если мы подставим в уравнение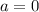
, то выполнится равенство:
Оба корня удовлетворяют уравнению и ОДЗ (при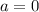
): с обеих сторон в первом случае получается 
, а во втором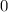 
(так как мы не выписывали ОДЗ, то мы могли получить "лишние корни", но мы их не получили).
Очевидно, что эти два корня в ответ так сразу не пойдут. Мы знаем лишь только, что они подходят при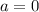
. И если ответ на задачу существует, то он может быть только 
, 
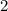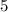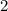или и 
, и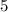 
. Но про другие значения 
мы пока ничего не знаем.
Посмотрим, что у нас будет получаться при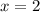
:
Вот только первый логарифм не всегда существует.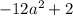
может быть отрицательным (возьмите, к примеру, 
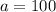). А подлогарифмическое выражение обязано быть положительным. Значит, такой 
нас не устраивает.
Теперь проверим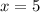
:
В обеих частях мы получили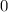
(так как 
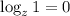, если 
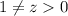). Также 
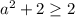, поэтому все ограничения будут выполняться.
В итоге имеем нужный ответ: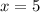
.
Задача решена!