1) Осевое сечение конуса - это равнобедренный треугольник.
У него боковые стороны - это образующие конуса, а в основании - диаметр основания конуса.
По условию каждый из двух углов при основании равен 60°, значит, и третий угол треугольника равен 60°.
180°-2·60°=60°
2) Итак, осевое сечение конуса - это равносторонний треугольник с периметром равным 24 см.
24 см : 3 = 8 см
 см - образующая конуса
см - образующая конуса
 см диаметр его
см диаметр его
 см
см
3) По теореме Пифагора находим высоту  .
.

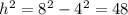
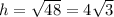
4) 

 =>
=>  см²
см²
5) 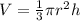


 см³
см³
ответ:  см² ≈ 144см²
см² ≈ 144см²
 см³ ≈ 108,8 см³
см³ ≈ 108,8 см³
В решении.
Пошаговое объяснение:
Найдите AD и AB, если периметр параллелограмма равен 108 см, AD-AB= 12см.
AD - x;
AB - y;
По условию задачи система уравнений:
х - у = 12
2(х + у) = 108
Сократить второе уравнение на 2 для упрощения:
х - у = 12
х + у = 54
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 12 + у
12 + у + у = 54
2у = 54 - 12
2у = 42
у = 42/2
у = 21 (см) - сторона АВ;
х = 12 + у
х = 12 + 21
х = 33 (см) - сторона AD;
Проверка:
Р = 2(33 + 21) = 2 * 54 = 108 (см), верно.
Пошаговое объяснение:
Осевое сечение конуса - равнобедренный треугольник, образованный двумя образующими и диаметром основания
Если угол у основания этого треугольника равен 60° то и второй угол у снования 60°, следовательно, угол у вершины равен 180° - 2*60° = 60°.
Поэтому образующая l = d = 24:3 = 8 (cм).
радиус основания r = d:2 = 8:2 =4 (см).
Тогда боковая поверхность конуса
Sб = π r l = π * 4 * 8 = 32π cм2
Площадь основания это круг, находим по формуле:
Sосн.= π r^2= π 4^2= 16π см2
Площадь полной поверхности:
Sп.п=Sб+Sосн= 32π +16π=48π см2
найдем высоту согласно т. Пифагора
h=√l^2-R^2=√8^2-4^2=√64-16=√48 =6,9 см
Объем равен:
V=1/3π r^2*h= 1/3π*4^2* 6,9= 36,8π см3