Question

Найдите сумму корней уравнения cosx x (sinx–cosx)=0, принадлежащих отрезку [– 180°; 360°].

Answer 1

90,270.-90 (если cosx=0)

или

45,225,-135 (если cosx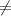$\neq$0)

Пошаговое объяснение:

Произведение двух выражений равно 0, если

1) первое выражение равно нулю, т.е. cosx=0;

2) второе выражение равно нулю, т.е. sinx-cosx=0.

Решим отдельно первый и второй случаи.

1) cosx=0 => x=p/2+pk

2)sinx-cosx=0 => Поделим обе части выражения на cosx, который не равен нулю(если бы cosx=0, то делить нельзя, т.к. нельзя делить на ноль).

Получим sinx/cosx-cosx/cosx=0

Знаем, что sinx/cosx=tgx

Поэтому получим

tgx-1=0

Далее

tgx=1

x=p/4+pk

Получили ответ:p/2+pk или p/4+pk

Нам необходимо выбрать те углы, которые находятся в промежутке от -180 до 360.

p/2+pk = 90 + 180k (где k - целое число).

Подставляя вместо к различные целые числа, выберем те, которые удовлетворяют условию(от -180 до 360). Получим, что это углы

90,270 и -90

Аналогично со вторым ответом.

p/4+pk = 45 + 180k

Получим углы 45, 225,-135