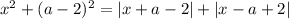
Рассмотрим правую часть уравнения.
Найдем нули модулей:
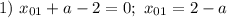
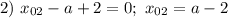
Тогда 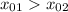 при
при 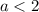 и
и 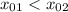 при
при 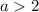 .
.
➠ Если 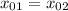 , то есть если
, то есть если 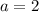 , то имеем:
, то имеем:
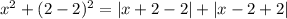
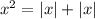
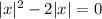
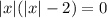
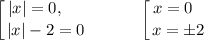
Имеем три корня. Таким образом, вариант 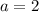 не подходит.
не подходит.
➠ Если 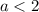 , то:
, то:
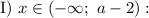
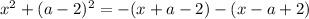
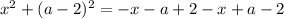
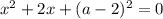
Имеем квадратное уравнение. Для того чтобы это уравнение имело один корень, нужно чтобы дискриминант данного уравнения был равен нулю:
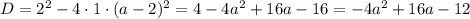
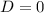 при
при 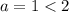 и
и 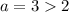
Таким образом, при 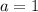 имеем решение.
имеем решение.
![\text{II}) \ x \in [a - 2; \ 2 - a]:](/tpl/images/1357/3941/2f10d.png)
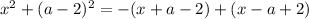
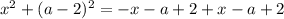
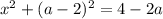
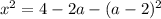
Данное квадратное уравнение будет иметь один корень, если его правая часть будет равна нулю:
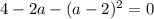
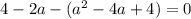
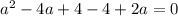
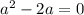
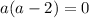
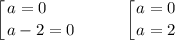
Таким образом, при 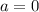 имеем единственное решение.
имеем единственное решение.
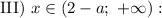
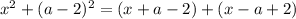
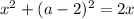
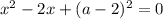
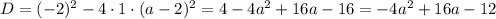
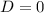 при
при 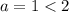 и
и 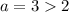
Таким образом, при 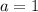 имеем решение.
имеем решение.
Следовательно, при 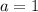 имеем два решения.
имеем два решения.
➠ Если 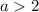 , то:
, то:
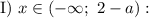
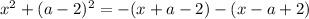
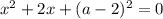
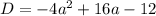
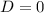 при
при 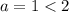 и
и 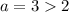
Таким образом, при 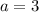 имеем решение.
имеем решение.
![\text{II}) \ x \in [2 - a; \ a - 2]:](/tpl/images/1357/3941/aa9bc.png)
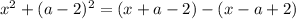
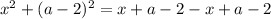
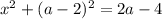
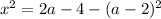
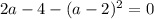
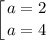
Таким образом, при 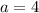 имеем единственное решение.
имеем единственное решение.
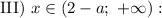
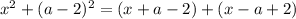
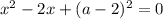
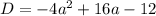
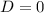 при
при 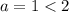 и
и 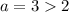
Таким образом, при 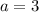 имеем решение.
имеем решение.
Следовательно, при 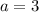 имеем два решения.
имеем два решения.
ответ: 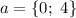

Пошаговое объяснение:
Задача 1.
1. После понижения цены на 10%, билет станет стоить:
35*0,9=31,5 руб
2. На 120 рублей можно будет купить:
120:31,5=3,8 ⇒ 3 билета.
ответ: 3 билета.
Задача 2.
1. (4-3i)/(2+i)=(4-3i)(2-i)/(2+i)(2-i)=(8-4i-6i-3i²)/(4-i²). Т.к. i²=-1, делаем замену:
(8-10i-3*(-1))/(4-(-1))=(8-10i+3)/5=(5-10i)/5=5(1-2i)/5=1-2i
2. (1+i)³=1³+3*1²*i+3*1*i²+i³=1+3i+3i²+i³. Т.к. i²=-1, делаем замену:
1+3i+3*(-1)+(-1)*i=1+3i-3-i=-2+2i
3. i³-i¹⁰⁰=i²*i-(i²)⁵⁰. Т.к. i²=-1, делаем замену:
(-1)*i-(-1)⁵⁰=-i-1
Задача 2.
1. (17-6i)/(3-4i)=(17-6i)*(3+4i)/(3-4i)*(3+4i)=(51-18i+68i-24i²)/(9-16i²). Т.к. i²=-1, делаем замену:
(51-50i-24*(-1))/(9-16*(-1))=(75+50i)/25
2. (1-i)³= 1³-3*1²*i+3*1*i²-i³=1-3i+3i²-i³. Т.к. i²=-1, делаем замену:
1-3i+3*(-1)-(-1)*i=1-3i-3+i=-2i-2
3. i^40-i^21=(i²)²⁰-i²⁰⁺¹. Т.к. i²=-1, делаем замену:
(-1)²⁰-(-1)²⁰*i=(-1)²⁰*(1-i)=1*(1-i)=1-i
Задача 4.
Пусть х - производительность первого рабочего, у - производительность второго рабочего, тогда 60/х-60/у=3.
За один час оба рабочих производят Х+у деталей.
Составим систему уравнений:
60/х-60/у=3
х+у=30
Первое упростим, из второго уравнения выразим х:
60(х+у)/ху=3 ⇒ 20(х+у)=ху
х=30-у
Подставим в первое уравнение выраженный х, решим уравнение:
20(30-у-у)=у(30-у)
600-40у=30у-у²
у²-70у+600=0
Д-70*70-4*600=2500
у₁=(70-50)/2=10 х₁=30-10=20
у₂=(70+50)/2=60 х₂=30-60=-30 - не удовлетворяет условию
Время , за которое второй рабочий производит 90 деталей: 90/10=9 часов.
ответ: 9 часов
Задача 5.
Пусть х - количество десятков, у - количество единиц. Составим систему уравнений:
у-х=2
(х+у)*(10х+у)=280
Выразим из первого уравнения у и подставим во второе.
у=2+х
(х+2+х)(10х+2+х)=280
Решим получившееся уравнение:
(2х+2)(11х+2)=280
22х²+4х+22х+4=280
22х²+26х-276=0
Д=26²+4*22*276=24964=158²
х₁=(-26+158)/(2*22)=3
х₂=(-26-158)/(2*22) <0 - не удовлетворяет условию
у=2+3=5
Искомое число: 35
ответ: 35
Введём параллелепипед ABCDA1B1C1D1 в прямоугольную систему координат OXYZ. Ноль в точке В, ось ОХ по ребру
ВА, ось ОУ по ребру ВС.
Прямая ВД1 задана двумя точками:
В(0, 0, 0).
Д1(12, 15, 16).
Задана точка А1(12, 0, 16).
Проекция точки А1 на прямую AB имеет координаты K(xk, yk, zk)
xk = 4800 / 625 = 192 / 25 = 7,68.
yk = 6000 / 625 = 48 / 5 = 9,6.
zk = 6400 / 625 = 256 / 25 = 10,24.
|А1K| = √(56250000) / 625 = 12.
Это расстояние было найдено по формуле:
|А1K| = √((xm-xs)*(xm-xs)+(ym-ys)*(ym-ys)+(zm-zs)*(zm-zs)).
Координаты векторов ВД1, ВA1 равны:
ВД1 = (12, 15, 16),
ВA1 = (12, 0, 16).
Координаты векторного произведения ВД1 и ВA1:
[ВД1х ВA1] = (240, 0, -180).
Модуль векторного произведения ВД1 и ВA1:
|[ ВД1х ВA1]| = √(90000) = 300.
Длина отрезка ВД1,
| ВД1| = √(625)= 25.
Расстояние от точки А1 до прямой ВД1 вычисляется по формуле
|А1K| = |[ ВД1х ВA1]| / |ВД1|.
|А1K| = √(90000 / 625) = √144 = 12.
Координаты проекции точки А1 на прямую ВД1:
K(192 / 25; 48 / 5; 256 / 25).
Расстояние от точки А1 до прямой ВД1:
|А1K| = 12.
a = 0 или a = 4
Пошаговое объяснение: