144°
Пошаговое объяснение:
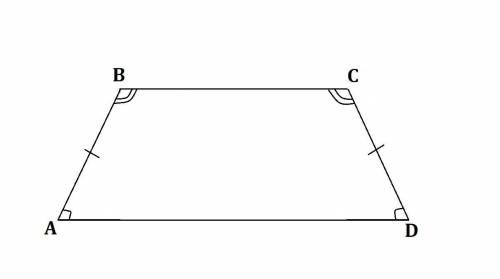
Обозначим данную трапецию буквами ABCD
По свойству равнобедренной трапеции ∠A = ∠D, ∠B = ∠C (также AB = CD)
По рисунку ∠B и ∠C - большие углы, ∠A и ∠D - меньшие углы.
****************
.1) Пусть x° - ∠A и ∠C, тогда 4x° - ∠B и ∠D.
Сумма внутренних углов любого четырёхугольника равна 360°.
4x + 4x + x + x = 360
10x = 360
x = 360: 10
x = 36
36° - меньший угол
Тогда 36° · 4 = 144° - больший угол
2) Можно было ещё по другому составить уравнение:
Пусть x° - ∠A, тогда 4x° - ∠B.
∠A и ∠B - внутренние односторонние при пересечении BC || AD секущей AB
⇒ ∠A + ∠B = 180°
x + 4x = 180
5x = 180
x = 180 : 5
x = 36
36° - меньший угол
Тогда 36° · 4 = 144° - больший угол.
.Так как ∠B > ∠A в 4 раза по условию, значит отношение большего угла к меньшему равно 4 : 1
4 + 1 = 5 (частей) - всего.
5 частей = 180°, так как ∠A + ∠B = 180° из 2)
180° : 5 = 36° - ∠A, то есть меньший угол
36° · 4 = 144° - ∠B, то есть больший угол
Пошаговое объяснение:
Приведите дроби 3/4; 4/6; 1/9; 3/18 к знаменателю 36.
27/36; 24/36; 4/36; 6/36
Ви відповіли правильно
Питання №2
/ a
Среди дробей 1/2; 2/3; 5/6; 3/7; 5/8; 9/11; 7/18; 9/24; 7/38 укажите такие, которые можно привести к знаменателю 72, умножив числитель и знаменатель дроби на целое число:
1/2; 2/3; 5/6; 5/8; 7/18; 9/24
Ви відповіли правильно
Питання №3
/ a
Приведите к наименьшему общему знаменателю дроби 3/8 и 4/15.
45/120 и 32/120
Ви відповіли правильно
Питання №4
/ a
Сравните дроби 7/9 и 8/11.
7/9>8/11
Ви відповіли правильно
Питання №5
/ ів
Укажите дробь, которая больше 1/4 и имеет знаменатель 16.
5/16
Ви відповіли правильно
Питання №6
/ ів
Расставьте в порядке возрастания числа 4/9; 1/4; 7/12; 13/18.
1/4; 4/9; 7/12; 13/18
Ви відповіли правильно
Питання №7
/ ів
Какие из дробей 3/7; 11/28; 1/2; 13/42; 23/70 больше дроби 5/14?
3/7; 11/28; 1/2
Ви відповіли правильно
Питання №8
/ ів
Найдите все натуральные значения x, при которых правильно неравенство
7;8;9;
Ви відповіли правильно
Заметим, что среди натуральных чисел от 1 до 10, для числа 7 может быть парой цифра 1 и только. Поэтому если выписали число 7, то оно будет скраю.
Число 5 может быть в паре с 1 или 10. Таким образом, если встречается число 5, то оно будет между 1 и 10.
Пока получается последовательность 7, 1, 5, 10.
В паре к 10 будет 2. Далее 6, 3, 9 или 4, 8 (для максимального кол-ва).
Получаем следующие последовательности:
7, 1, 5, 10, 2, 6, 3, 9 (8 чисел);
7, 1, 5, 10, 2, 4, 8 (7 чисел).
Если бы число 5 не встречалось, то максимум получилось 10-1-1=8 чисел.
А теперь, рассмотрим случай, когда число 7 не выписывали. Тогда максимум может быть 10-1=9 чисел.
5, 10, 1, 9, 3, 6, 2, 4, 8 (9 чисел).
Наибольшее количество чисел 9.
ответ: 9.