1.6
Пошаговое объяснение:
поскольку α ∈ [пи;3пи\2], то косинус имеет знак "-"

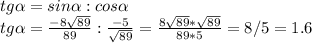
ответ:
симметрия — слово греческого происхождения, как и многие другие слова, которые связаны с . оно означает соразмерность, наличие определённого порядка, закономерности в расположении частей. смотря на объекты вокруг, мы не раз восклицаем: «какая симметрия! »
aksiala9.jpg
люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.
111.jpg
пока рассмотрим две симметрии на плоскости: относительно точки и прямой.
центральная симметрия
симметрию относительно точки называют центральной симметрией.
точки m и m1 симметричны относительно некоторой точки o , если точка o является серединой отрезка mm1 .
simetrija_c_punkti.png
точка o называется центром симметрии.
алгоритм построения центрально-симметричных фигур.
simetrija_c.png
построим треугольник a1b1c1 , симметричный треугольнику abc относительно центра (точки) o :
1. для этого соединим точки a , b , c с центром o и продолжим эти отрезки;
2. измерим отрезки ao , bo , co и отложим с другой стороны от точки o равные им отрезки ao=oa1; bo=ob1; co=oc1 ;
3. соединим получившиеся точки отрезками и получим треугольник a1b1c1 , симметричный данному треугольнику abc .
фигуры, симметричные относительно некоторой точки, равны.
фигура симметрична относительно центра симметрии, если для каждой этой точки фигуры симметричная ей точка также лежит на этой фигуре. такая фигура имеет центр симметрии (фигура с центральной симметрией).
есть фигуры с центральной симметрией, это, например, окружность и параллелограмм. у окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. есть много фигур, у которых нет центра симметрии.
осевая симметрия
осевая симметрия — это симметрия относительно проведённой прямой (оси).
точки m и m1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
simetrija_ass_punkti.png
алгоритм построения фигуры, симметричной относительно некоторой прямой.
simetrija_ass.png
построим треугольник a1b1c1 , симметричный треугольнику abc относительно красной прямой:
1. для этого проведём из вершин треугольника abc прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. соединим получившиеся точки отрезками и получим треугольник a1b1c1 , симметричный данному треугольнику abc .
фигуры, симметричные относительно прямой, равны.
фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. прямая является в этом случае осью симметрии фигуры
ответ:
пошаговое объяснение: ) назовём левую часть у. максимальное значение левой части у-1. сначала найдём у, т.к. мы можем это сделать: 1)767520: 4=191880. 2)191880: 15=12792. 3)12792: 123=104. правая часть=104. максимальное значение левой части 104-1=103. ответ: 103
б)сделаем то же самое, но теперь максимальное значение левой части равно у. найдём у. но сначала умножим 96*16. 1) 96*16=1536.
2)319499: 1536=208 целых 11/1536. умножим на 505. 208 11/1536*505=105040 целых 5555/1536=105043 целых и ещё что то. т.к. нам надо натуральное наибольшим решением будет 105043. ответ: 105043
2)найдём косинус используя основное тригонометрическое свойство:
Sin^2+Cos^2=1;
Далее выразим искомый косинус:
Cos^2=1-sin^2
Подставляешь числа, находишь косинус и потом просто подставляешь в формулу под пунктом 1.