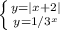
Данная система эквивалентна уравнению :
3^(-x) =|x+2|
3^(-x) -|x+2| = 0
3^(-x) +-(x+2) = 0 , в зависимости от знака выражения x+2
Найдем производную f(x) = 3^(-x) +-(x+2)
f'(x) = -3^(-x) *ln(3) +-1
1) x+2 >=0
f'(x)= -3^(-x) *ln(3) -1 <= 0 - функция монотонно убывает
2) x+2<0 ; x<-2
f'(x) = -3^(-x) *ln(3) +1
При x<-2 ; -x > 2 ⇒ -3^(-x) <- 3^2 = -9
Поскольку : 3>e , то ln(3) >1 ⇒ -3^(-x) *ln(3) < -9 ⇒ -3^(-x) *ln(3) +1 <- 8 - функция монотонно убывает.
Вывод : Данная система эквивалентна уравнению :
3^(-x) =|x+2|
3^(-x) -|x+2| = 0
3^(-x) +-(x+2) = 0 , в зависимости от знака выражения x+2
Найдем производную f(x) = 3^(-x) +-(x+2)
f'(x) = -3^(-x) *ln(3) +-1
1) x+2 >=0
f'(x)= -3^(-x) *ln(3) -1 <0 - функция монотонно убывает
2) x+2<0 ; x<-2
f'(x) = -3^(-x) *ln(3) +1
При x<-2 ; -x > 2 ⇒ -3^(-x) <- 3^2 = -9
Поскольку : 3>e , то ln(3) >1 ⇒ -3^(-x) *ln(3) < -9 ⇒ -3^(-x) *ln(3) +1 <- 8 - функция монотонно убывает.
Вывод : функция монотонно убывает на множестве действительных чисел .
Заметим, что f(-1) = 3^1 -|1| = 2>0 ; f(0)= 3^0 -|2| = 1-2 =-1<0
Данная функция может иметь горизонтальные ассимптоты, однако, поскольку функция монотонно убывает на множестве действительных чисел, то может иметь не более одной ассимптоты при возрастании аргумента и не более одной ассимптоты при убывании аргумента. Таким образом, поскольку f(-1) >0 и f(0) < 0 и функция монотонно убывает на множестве действительных чисел, уравнение
3^(-x) -|x+2| = 0 имеет единственное решение, которое лежит на промежутке x∈(-1;0), как и представленная система уравнений.
На рисунке 1 показан график функции f(x).
Второй аналитически-графический)
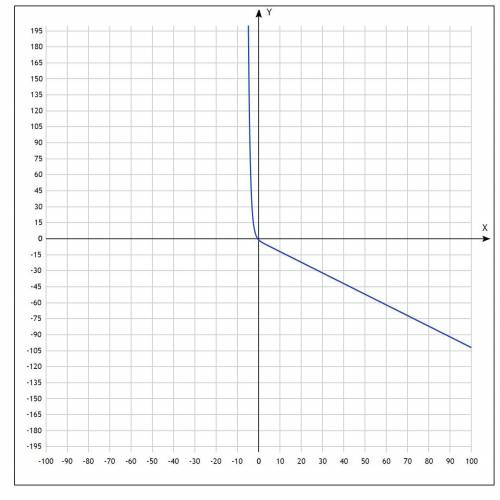
На рисунке 2 показаны графики функций: y= 1/3^x = 3^(-x) и |x+2| в одной системе координат. В силу геометрических соображений при построении графиков, очевидно, что правая ветка модуля точно пересекает график степенной функции и ровно в одной точке. Таким образом одно решение уже существует.
Так же , но уже менее очевидно, левая ветка модуля не пересекает степенную функцию. Это необходимо доказать.
Докажем, что при любом x<-2 (область определения левой ветки модуля) степенная функция больше чем левая ветка модуля, то есть :
f(x) =3^(-x) - (-x-2) >= 0
Доказать это можно двумя
1) Интуитивно :
f(-2) = 3^2 -|0| = 9 >0
Из графика видно , что при убывании аргумента от -2 оба графика возрастают, но при этом степенная функция растет быстрее линейной, то есть f(x) > 9 , то есть левая ветка модуля не пересекает степенную функцию.
Вывод : cистема имеет единственное решение.
2) Cтрого.
Cкорость роста линейной функции при УБЫВАНИИ аргумента на x<-2 (-x-2) постоянна и
равна u= -(-x-2)' = 1
А у показательной функции скорость увеличивается :
v = -(3^(-x) )' = 3^(-x)* ln(3)> 9*ln(3) > u , при x<-2.
Тогда, поскольку f(-2)= 9 > 0 , то степенная функция больше линейной при x<-2
Пошаговое объяснение:
2х-3у=6, т.к. ни один из коэффициентов при переменных не равен нулю,то графиком будет прямая.Чтобы построить прямую надо знать минимум две точки.Подставим в уравнение Х и получим значение У и наоборот.
ели х=0 подставляем вместо х 0,
2*0-3у=6
-3у=6
у=6:(-3)
у=-2
теперь у=0 подставляем в уравнение
2х-3*0=6
2х=6
х=6:2
х=3
и так получили две точки графика (0;-2) и (0;3)
Теперь чертим координатную плоскость и отмечаем наши точки,проведём через них прямую это и будет графиком уравнения 2х-3у=6
А значит на области задания f(x) монотонно убывает.
А значит на области задания g(x) монотонно возрастает, а s(x) монотонно убывает. А значит при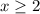 имеют не более одной точки пересечения.
имеют не более одной точки пересечения.
Т.к.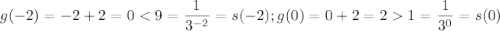 , то эта точка пересечения существует, причем принадлежит интервалу
, то эта точка пересечения существует, причем принадлежит интервалу 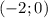 .
.
А значит исходная система имеет одно решение