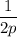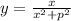
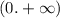
Вися́чие сады́ Семирами́ды — одно из Семи чудес античного мира, которое представляло собой инженерное сооружение в Вавилоне с каскадом многоуровневых садов, где росли многочисленные породы деревьев, кустарников и виноградных лоз, производившее впечатление большой зелёной горы. Единственное из Семи чудес, местонахождение которого окончательно не установлено[1] и, более того, подвергается сомнению сам факт его существования[⇨], поскольку не сохранилось никаких вавилонских текстов, в которых упоминаются эти сады, описания садов имеются лишь у поздних древнегреческих и римских авторов[⇨], а археологические раскопки в районе предполагаемого местонахождения садов также не дали результато
Пошаговое объяснение:
Егер ондық жүздік бөлшекті дөңгелектіегні келсе былай болады !
Ең соңғы сан 5 6 7 8 9 болса ол алдынғы тұрған санды бір санға үлкейтеді яғни бір саның екіге айналдыарады! Түсінікті болуы үшін,мысал келтірейін!
Мысалға:
0,44415 = 0,4442 көріп тұрғанындай 5 саны алддында тұрған 1ді екіге айналдырып жіберді!
Келесі мысал:
10,6788881114888888 = 10,6788881115
10,6788881114888888 = 10,678888111488889
10,6788881114888888 = 10,67888811148889
10,6788881114888888 = 10,6788881114889
10,6788881114888888 = 10,678888111489
10,6788881114888888 = 10,67888811149
Жауабым түсінікті болса, Рахметінді аяма)))
Заметим, что для рассмотрения функции можно считать, что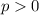 , так как в функцию
, так как в функцию 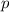 входит в четной степени
входит в четной степени
Найдем производную:
Найдем точки, в которых производная равна нулю:
На промежутке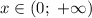 с учетом уточнения
с учетом уточнения 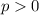 такая точка одна:
такая точка одна:
Найдем точки, в которых производная не существует:
Равенство выполняется при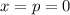 , однако эта точка не попадает в заданный промежуток
, однако эта точка не попадает в заданный промежуток 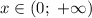
Таким образом, нужно проверить наличие экстремума в точке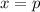 .
.
Найдем знаки производной в точках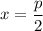 и
и 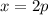 :
:
Значит:
при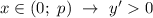
при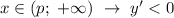
Таким образом, при переходе через точку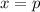 производная меняет знак с "плюса" на "минус". Значит,
производная меняет знак с "плюса" на "минус". Значит, 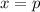 - точка максимума. Найдем значение максимума:
- точка максимума. Найдем значение максимума:
Поскольку заданный промежуток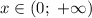 не отрезок, то проверим, что предел при стремлении
не отрезок, то проверим, что предел при стремлении  к границам промежутка не больше полученного максимума:
к границам промежутка не больше полученного максимума:
Оба предела равны 0. Значит,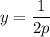 - наибольшее значение функции на заданном промежутке.
- наибольшее значение функции на заданном промежутке.
ответ: