Question

На доске выписаны различные числа делящиеся на 3 и оканчивающиеся на 2. Найдите наибольшее количество слагаемых чтобы получить число 1164

Answer 1

7

Пошаговое объяснение:

Первое число, удовлетворяющее условиям, равно 12. Чтобы число делилось на 3, сумма его цифр должна делиться на 3. Последняя цифра постоянна — это 2, значит, сумма остальных цифр должна при делении на 3 давать остаток 1, что уже верно для числа 12. Значит, все подходящие числа можно описать следующей формулой (утверждение 1):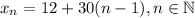 $x_n=12+30(n-1), n\in\mathbb{N}$. Увеличение числа на 30 не изменяет последнюю цифру, при этом каждый раз сумма цифр без последней изменяется на 3 — наименьшее натуральное число, которое не меняет остаток от деления на 3.

Сумма данных чисел оканчивается на 4, если количество чисел при делении на 5 даёт остаток 2 (утверждение 2). Действительно, сумма пяти двоек оканчивается на 0 (меньшим количеством двоек получить 0 невозможно), да ещё две двойки дают на конце 4.

Слагаемых тем больше, чем меньше каждое из чисел. Если записать числа по порядку, то первое число не меньше 12, второе — не меньше 42 и т. д., то есть максимально возможное количество слагаемых достигается, если последовательность задана формулой из утверждения 1. Тогда их сумма — это сумма арифметической прогрессии:

$S_{\min}=\dfrac{2\cdot 12+30(n-1)}{2}\cdot n=15n^2-3n\leq 1164\Leftrightarrow 5n^2-n-388\leq 0\\\dfrac{1-\sqrt{7761}}{10}\leq n\leq \dfrac{1+\sqrt{7761}}{10}$

C учётом натуральности n ≤ 8. По утверждению 2 n = 2 или n = 7.

Пусть n = 7. Пусть записаны числа 42, 72, 102, 132, 162, 192, 462. Каждое из них делится на 3, их сумма равна 1164.