Question

Xy(x+y)+yz (y-z)-xz (x+z) разложить на множители​

Answer 1

$(y-z)(x+y)(x+z)$

Пошаговое объяснение:

1. Нужно умножить и объединить подобные члены:

$xy^{2} -xz^{2} +yx^{2} -yz^{2} -zx^{2} +zy^{2}$

2. Потом рассмотреть выражение выше как переменный x:

$(y-z)x^{2} +(y^{2} -z^{2} )x-yz^{2} +zy^{2}$

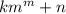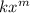3. Находим один множитель в форме: $km^{m} +n$, где $kx^{m}$ делит одночлен с наибольшим значением 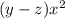$(y-z)x^{2}$, а n делит постоянный множитель 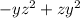$-yz^{2} + zy^{2}$. Один из таких множителей - это 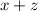$x+z$. Потом нужно разложить полином, разделив его на этот множитель:

$(x+z)(xy-xz+y^{2} -yz)$

4. Мы должны учесть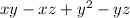 $xy-xz+y^{2} -yz$. Выполняем группировку 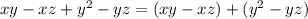$xy-xz+y^{2} -yz=(xy-xz)+(y^{2} -yz)$, а затем нужно вынести за скобки x в первой и y во второй группе:

$x(y-z)+y(y-z)$

5. Надо вынести за скобки общий член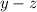 $y-z$, используя свойство дистрибутивности.

$(y-z)(x+y)$

6. В последний шаг нужно переписать полное разложенное на множители выражение:

$(x+y)(x+z)(y-z)$