Пусть скорость мотоциклиста из пункта А до В равна х км/ч
весь путь вычисляется по формуле
S=vt
Тогда время в часах затраченное мотоциклистом от А до В равно
t = S/x
а время от В до А равно
S/2÷ (x+9)+S/2÷30
так как время обратного пути мотоциклиста равно первоначальному, то получаем следующее уравнение
S/x = S/2÷ (x+9)+S/2÷30
Делим обе части уравнения на S, т.к. знаем, что S, не равно 0
переносим в одну сторону. Получаем следующее уравнение
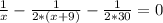
приведем к общему знаменателю
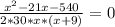
Дискриминант равен (-21)²-4*1* (-540)= 2601
Д больше 0, значит уравнение имеет 2 корня

Так как скорость не может быть отрицательным числом, значит
ответ 36 км/ч
Пусть всего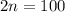 точек. Рассмотрим граф на этих вершинах. Рассмотрим вершину (пусть это вершина
точек. Рассмотрим граф на этих вершинах. Рассмотрим вершину (пусть это вершина 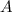 ) с наибольшей степенью. Пусть эта степень равна
) с наибольшей степенью. Пусть эта степень равна  . Заметим, что у вершин, имеющих связь с
. Заметим, что у вершин, имеющих связь с 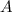 нет ребер к другим вершинам, связанным с
нет ребер к другим вершинам, связанным с 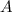 (иначе получился бы треугольник). Поэтому степень этих вершин не больше, чем
(иначе получился бы треугольник). Поэтому степень этих вершин не больше, чем  . Степени оставшихся не превосходят
. Степени оставшихся не превосходят  . Поэтому сумма степеней не превосходит
. Поэтому сумма степеней не превосходит 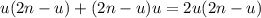 . Количество ребер не превосходит
. Количество ребер не превосходит 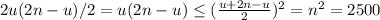 (последнее неравенство — следствие из н-ва между ср. арифм. и ср. геометр.)
(последнее неравенство — следствие из н-ва между ср. арифм. и ср. геометр.)
С другой стороны, несложно привести пример: рассмотрим двудольный граф (две равные доли по 50 вершин) и проведем всевозможные ребра (их будет 50*50=2500).
Если же проведено более 2500 ребер, то образуется хотя бы один треугольник (на самом деле их будет хотя бы 50).
ответ: 2500