Question

ЕЩЕ ОДИН ВОПРОС . что нужно делать , если с условием анологичным этому номеру , но только просят найти с различными корнями , то что мне требуется делать? А ЕЩЕ
ребята , я скоро сдаю экзамены , в одно очень важное для меня место , куда я очень сильно хочу.И вот у меня были в начале года пробные экзы , а я тогда считала что они очень легкие и посчитала нужным не готовиться , но видимо с самоуверенностью переборщила , но с июня я взяла себя в руки и начала готовится , и теперь не успеваю химию..Мне страшно ужасно , я не знаю как избавится от этого страха , дайте совет лишний совет мне не помешает..​

Answer 1

5х²-kx+5=0

Два различных корня в этом квадратном уравнении будут при D>0

k²-4*5*5>0   метод интервалов

k²-10²=0    парабола ветвями вверх

(k-10)(k+10)=0;  k1=10; k2=-10

Точки -10 и 10 пустые, т.к. неравенство строгое.

(-10)(10)>k

    +                     -                   +

ответ: к∈(-∞; -10)U(10; ∞)          C).

Answer 2

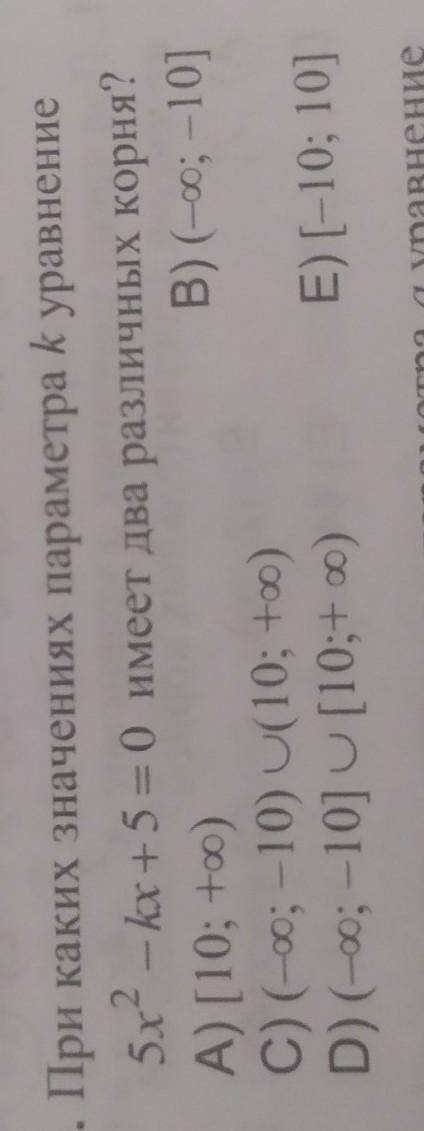
5х²-кх+5=0

Обычное квадратное уравнение. Поэтому когда у него различные два корня? Когда дискриминант больше нуля.  к²-4*5*5>0

(к-10)*(к+10)>0, решим неравенство методом интервалов, разбив на интервалы числовую ось корнями левой части к=10, к=-10, и установив знаки на каждом интервале. Нас будут интересовать интервалы, на которых мы поставим плюс.

-1010

    +             -          +

т.о., к ∈(∞;-10)∪(10;+∞)

Верный ответ С.