Можно рассуждать так.
Часовая стрелка между 5 и 6 часами, а минутная отстает, значит еще не 5:30. Часовая стоит или на 1 делении после 5 или на втором.
Если на первом делении, то это 5:12 , а минутная стоит на 3 деления позади, это 23 минуты. Не сходится.
А вот если часовая стрелка стоит на 2-ом делении после 5 часов, то это 5:24, т.к 1 час:5=60:5=12 минут. Тогда минутная на 3 деления сзади, это 2 деления до 5-ти и одно после 5-ти ближе к 4 часам. Как раз 24 минуты.
ответ: 5:24. Ну, или 17:24.
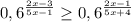
Показательная функция с основанием (0 <0,6 <1) убывающая, значит большему значению функции соответствует меньшее значение аргумента
Это означает, что в неравенстве между показателями степеней знак меньше:
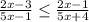
Получили дробно- рациональное неравенство.
Переносим выражение справа в левую часть
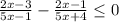
Приводим к общему знаменателю и получаем неравенство
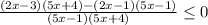
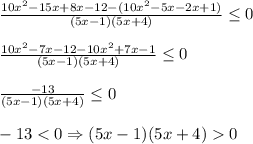
Знаменатель дроби не должен равняться 0, поэтому неравенство строгое.
Решение неравенства x < -4/5 или x>1/5
Интервалов два:
(-∞;-4/5) U (1/5;+∞)
Наименьшее целое положительное х=1
В ответ не вошли числа принадлежащие
[-4/5;1/5]
Далее непонятен вопрос, сумму каких чисел надо найти:
целых положительных?
преобразуем :
a) sin(5пи/14)*cos(пи/7)+cos(5пи/14)*sin(пи/7) = sin(5пи/14 + пи/7)= sin(пи/2) = 1
б) cos 78 градусов cos 18 градусов + sin 78 грудусов sin 18 градусов = cos(78 градусов - 18 градусов) = cos(60 градусов) = 1/2.
2)
У выражения
а) sin альфа cos бета - sin (альфа - бета)
sin (альфа - бета) = sin (альфа) * cos (бета) - cos (альфа) * sin (бета) , тогда получим :
sin альфа cos бета - sin (альфа - бета) = sin альфа * cos бета - sin (альфа) * cos (бета) - cos (альфа) * sin (бета) = - cos (альфа) * sin (бета) , поэтому :
sin альфа cos бета - sin (альфа - бета) = - cos (альфа) * sin (бета) .
б) cos ( пи\3 + x) + (корень из 3)\2 sin x - исходное выражение, преобразуем его :
cos ( пи\3 + x) = cos ( пи\3) *cos (х) - sin( пи\3) * sin(x) = cos (х) /2 - (корень из 3)\2 *sin(x) , тогда получим :
cos ( пи\3 + x) + (корень из 3)\2 sin x = cos (х) /2 - (корень из 3)\2 *sin(x) + (корень из 3)\2 sin x = cos (х) /2.
3) Докажите тождество :
cos (альфа+бета) - cos (альфа- бета) = - 2 sin альфа sin бета - исходное выражение, которое преобразуем ,
используя формулы сложения тригонометричесикх функций:
cos (альфа+бета) = cos (альфа) *cos (бета) - sin альфа sin бета,
cos (альфа-бета) = cos (альфа) *cos (бета) + sin альфа sin бета, суммируя выражения получим :
cos (альфа+бета) - cos (альфа- бета) = cos (альфа) *cos (бета) - sin альфа sin бета - cos (альфа) *cos (бета) - sin альфа sin бета =
= - 2 sin альфа sin бета.
что требовалось доказать .
4) решите уравнение
cos 4x cos x + sin 4 x sinx=0
Используя те же формулы, получим :
cos 4x cos x + sin 4 x sinx = cos (4x - x)= cos 3x, тогда
cos 3x = 0, при
3x = (( 2*n +1 )/2) * пи, отсюда :
x = (( 2*n +1 )/6) * пи
Пошаговое объяснение:
17:24
Пошаговое объяснение:
Найдём скорость часовой стрелки в минутах: 5/60 = 1/12 - т.е. часовая стрелка проходит за расстояние равное 1-ому делению минутной стрелки за 12 минут. А скорость минутной стрелки равна 1. В 17:00 часовая стрелка находится впереди минутной на 25 делений.
Скорость с которой минутная стрелка догоняет часовую:
Отсюда находим время: (25-3 - это расстояние которое по условию проходит минутная стрелка.)
(25-3 - это расстояние которое по условию проходит минутная стрелка.)
Отсюда 17:24