Решение квадратных уравнений
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
Не имеют корней;
Имеют ровно один корень;
Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант. Дискриминант Пусть дано квадратное уравнение ax2 + bx + c = 0. Тогда дискриминант — это просто число D = b2 − 4ac.Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Если D < 0, корней нет;
Если D = 0, есть ровно один корень;
Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:Задача. Сколько корней имеют квадратные уравнения:
x2 − 8x + 12 = 0;
5x2 + 3x + 7 = 0;
x2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8)2 − 4 · 1 · 12 = 64 − 48 = 16 Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 32 − 4 · 5 · 7 = 9 − 140 = −131.Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6)2 − 4 · 1 · 9 = 36 − 36 = 0.Дискриминант равен нулю — корень будет один.Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.Корни квадратного уравнения Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:Формула корней квадратного уравнения Основная формула корней квадратного уравнения Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D < 0, корней нет — ничего считать не надо.
Пошаговое объяснение:
1)
1:9=0,111111...
4:11=0,363636...
47:12=3,91 6666..
12,4 : 27=0.45925925..
2)
5/12=0,4166666..=0,41(6)
11/15=0,733333...=0,7(3)
9/11=0,81818181..=0,(81)
19/36=0,527777..=0,52(7)
39/44=0,88636363..=0,88(63)
3)
3/11 и 0,269
3/11=0,272727=0,(27)
0,(27) > 0,269 значит 3/11 > 0,268
7/9 и 77/100
7/9=0,7777..=0,(7)
77/100=0,77
0,(7) > 0,77 значит 7/9 > 77/100
11/12 и 19/20
11/12=0,91666..=0,91(6)
19/20=0,95
0,91(6) < 0,95 значит 11/12 < 19|20
47/15 и 119/36
47/15=3,1333..=3,1(3)
119/36=3,30555..=3,30(5)
3,1(3) < 3,30(5) значит 47/15 < 119/36
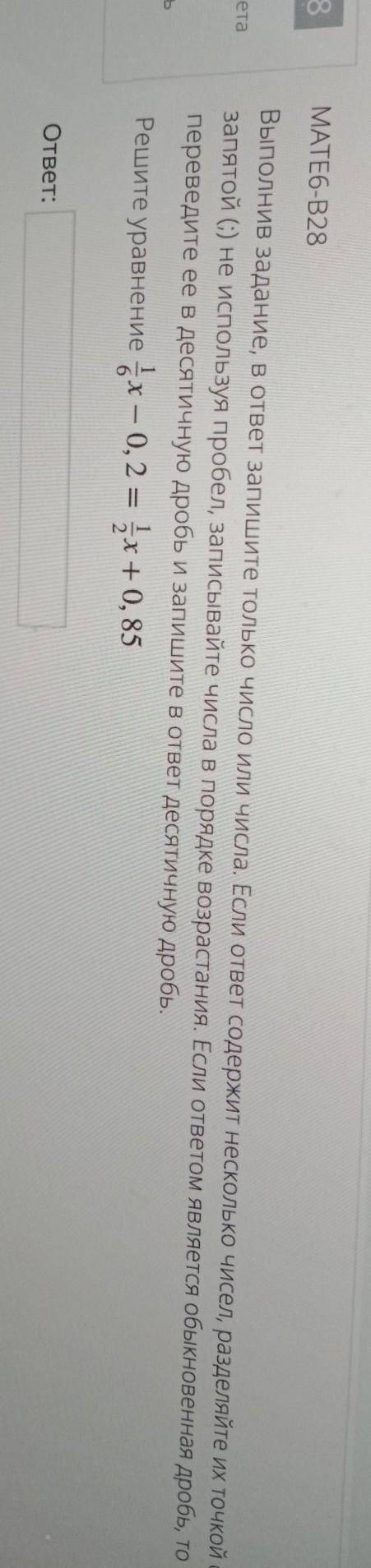
Переносим все по сторонам: 1/6х-1/2х=0.85+0.2 Приводим все, получаем: -1/3х=1.05 х=1.05/ (-1/3) х=-3.15