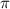 ≈3,1)
≈3,1)Раз область значений функций левой и правой части уравнения 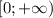 , то, приравняв левую и правую части уравнения к нулю, получим
, то, приравняв левую и правую части уравнения к нулю, получим 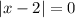 и
и 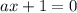 откуда
откуда 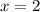 и
и  - одно решение
- одно решение
Левая часть - под коренное выражение неотрицательно, т.е. уравнение будет зависеть только от правой части.
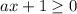
Возводим левую и правую части уравнения в квадрат
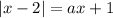
При условии, что 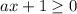 , возводим снова в квадрат обе части уравнения:
, возводим снова в квадрат обе части уравнения:
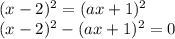
В левой части применим формулу разности квадратов:
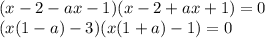
Произведение равно нулю, если хотя бы один из множителей равен нулю.
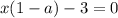 откуда
откуда 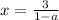
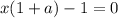 откуда
откуда 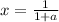
Теперь исследуем на условии 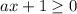 . Подставляем первый корень
. Подставляем первый корень
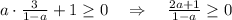
Решением этого неравенства является промежуток 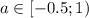
Подставим теперь второй корень.
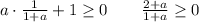
решением этого неравенства является промежуток ![a \in (-\infty;-2]\cup(-1;+\infty)](/tpl/images/0922/4683/afe62.png)
Пересечение этих двух решений: 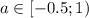 . Из выше сказанного при а = -0,5 уравнение имеет одно решение. Поэтому при
. Из выше сказанного при а = -0,5 уравнение имеет одно решение. Поэтому при  данное уравнение имеет более одного решения.
данное уравнение имеет более одного решения.
ответ: при a ∈ (-0.5;1).
нет
Пошаговое объяснение:
длина стороны прямоугольника должна быть меньше двух радиусов круга.
площадь круга равна S=π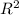 ;
;
2R=2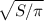 ;
;
2R=3.2 см, это больше, чем длина стороны.