1). Для приготовления варенья из смородины, количество всех продуктов отмеряют стаканами. При этом ягоды составляют 3/7, а сахар и вода соответственно и 1/2 и 1/14 от всего количества. Рассчитайте,сколько стаканов сахара и воды необходимо взять, если для варенья собрано 30 стаканов смородины. 2) Для изготовления ковра требуется шерстяные нитки четырех цветов: 1/10 всех ниток должна быть красного цвета, 2/5 - синего, 3/20 — коричневого и остальные- белого. Сколько граммов ниток каждого цвета потребовалось для изготовления ковра, если на него ушло 700 г белых ниток?

👇

Увидеть ответ

Ответ:

urkashkz777

13.03.2023

1) расчитаем сколько всего различных продуктов было исходя из количества смородины

30:3*7=70 стаканов

найдем количество сахара

70:2*1=35 стаканов

найдем количество воды

70:14*1=5 стаканов

проверяем 30+35+5=70 стаканов

2) 1-(1/10+2/5+3/20)=1-(2/20+8/20+3/20)=7/20 (всех ниток) - белые, это 700г;

700 :7*20= 2000 (г) - всего;

2000 :10= 200(г) - красные;

2000:5*2 =800 (г) -синие;

2000:20*3= 300(г.)- коричневые.

4,6(88 оценок)

Ответ:

JeanSu

13.03.2023

1) 35 стаканов сахара, 5 стак.воды;

2) 200 гр- ниток красного цвета,

800 гр - синего,

300 гр - коричневого.

Пошаговое объяснение:

По условию количество смородины 3/7, что равно 30 стаканам. Исходя из этого вычисляем, что 1 стакан смородины равен-

3/7:30=3/7*1/30=1/70;

Вычисляем количество сахара-

1/2:1/70=1/2*70/1=35 (стаканов);

Вычисляем количество воды-

1/14:1/70=1/14*70/1=5 (стаканов).

Проверка:

30+35+5=70 (стаканов всего)

2) Всего ниток 1 целая - х;

Ниток красного цвета - 1/10х;

Синего - 2/5х;

Коричневого-3/20х;

Остальные по условию белые-700 гр

Уравнение:

х-1/10х-2/5х-3/20х=700

(20-2-8-3)х/20=700

7/20х=700

х=700:7/20=700*20/7

х=2000 (гр - ниток всего)

1/10*2000=200 (гр - красных ниток)

2/5*2000=800 (гр - синих ниток)

3/20*2000=300 (гр - коричневых)

Проверка:

2000-200-800-300=700 (белых нит.)

4,4(46 оценок)

Открыть все ответы

Ответ:

mariazeleznak2

13.03.2023

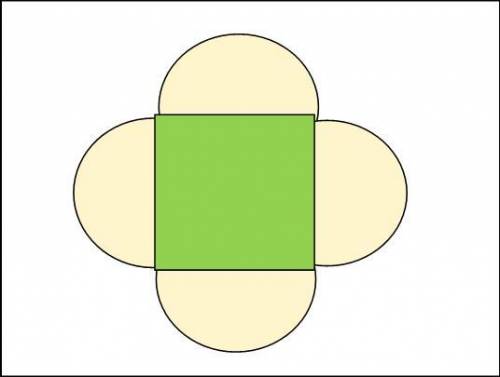
Пусть (м) - сторона квадрата, тогда

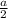$\frac{a}{2}$ (м) - длина радиуса полукругов

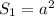S_1=a^2 (м²) - площадь квадрата

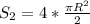$S_2=4*\frac{\pi R^2}{2}$ (м²) - площадь 4-х полукругов через радиус

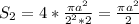$S_2=4*\frac{\pi a^2}{2^2*2}= \frac{\pi a^2}{2}$ (м²) - площадь 4-х полукругов через /

Теперь выразим площадь 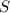всей клумбы:

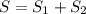
S=S_1+S_2

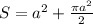
$S=a^2+\frac{\pi a^2}{2}$

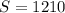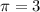По условию S=1210 м² и $\pi =3$ , поставим в последнее уравнение и найдем .

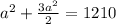
$a^2+\frac{3a^2}{2}=1210$

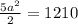
$\frac{5a^2}{2}=1210$

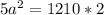
5a^2=1210*2

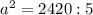
a^2=2420:5

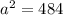
a^2=484

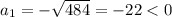
$a_1=-\sqrt{484}=-22$

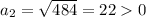
$a_2=\sqrt{484}=220$

ответ первый: 22 м - длина стороны квадрата.

22 : 2 = 11

ответ второй: 11 м - длина радиуса полукругов.

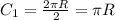$C_1=\frac{2\pi R}{2}=\pi R$ длина одного полукруга.

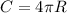$C=4\pi R$ длина 4-х полукругов, она же и есть длина декоративного забора.

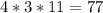
4*3*11=77

ответ третий: 77 м - длина декоративного забора.

В городе была сделана цветочная клумба, образованная из квадрата и четырёх полукругов. Площадь клумб

4,4(43 оценок)

Ответ:

anya071101

13.03.2023

Пошаговое объяснение:

Есть два метода решения системы уравнений

1-метод подстановки, когда значение либо (х,) либо ( у) одного из уравнений подставляться в другое уравнение.

2 метод алгебраического сложения, два уравнения складываються, если в одном уравнении (х) или (у) положительные,а во втором отрицательные, при этом множители их должны быть одинаковыми.

1) уравнение мы будем решать с подстановки

{у=1-7х

4х-у=32

у=1-7х это значение поставим во второе уравнение вместо у

{у=1-7х

4х-(1-7х)=32

Решаем второе уравнение

4х-1+7х=32

11х-1=32

11х=32+1

11х=33

х=33:11

х=3

Теперь значение х, которое мы нашли, подставляем в первое уравнение и решаем его

у=1-7х

у=1-7•3

у=1-21

у=20

ответ (3;20)

2)Второе уравнение мы тоже,будем решать с подстановки

{х=4у

х+5у=99

Подставляем значение х первого уравнения, во второе уравнение

х+5у=99

4у+5у=99

9у=99

у=99:9

у=11

Подставляем значение у в первое уравнение

х=4у

х=4•11

х=44

ответ (44;11)

3) уравнение будем решать методом сложения

{7х-2у=15

2х+у=9

У нас есть (-2у) первого уравнения,и у второго уравнения, для того чтобы они взаимоуничтожились, необходимо привести их к общему множителю. т.е. к 2.

{7х-2у=15 оставляем как есть

2х+у=9 умножаем все уравнение на 2

{7х-2у=15

2•2х+2•у=2•9

{7х-2у=15

4х+2у=18 складываем два уравнения

между собой

7х+4х-2у+2у=15+18

11х=33 (у взаимоуничтожаются, т.к. они с разными знаками)

11х=33

х=33:11

х=3

Подставляем значение х в одно из уравнений

2х+у=9

2•3+у=9

6+у=9

у=9-6

у=3

ответ: (3;3)

{2(х+у)=8

14-3(х-у)=5у-х

Вначале открываем скобки и решаем.

{2х+2у=8

14-3х-3у=5у-х

Переносим все значения х и у вправо от равно, а все известные влево. При переносе за знак равенства (=) ,знаки меняются на противоположные

{2х+2у=8

-3х-3у-5у+х=-14

{2х+2у=8

-2х-8у=-14

Поскольку у нас есть в первом уравнении (2х) положительная, а во втором (-2х) отрицательная, нам легче использовать метод сложения, где эти значения взаимоуничтожаются.

{2х+2у=8

-2х-8у=-14

Складываем эти два уравнения между собой

2х-2х+2у-8у=8-14 (х взаимоуничтожаются)

-6у=-6

у=-6:(-6)

у=1

Подставляем значение у в одно из уравнений

2х+2у=8

2х+2•1=8

2х+2=8

2х=8-2