Пошаговое объяснение:
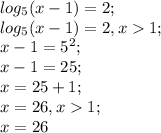
Проверка:
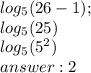
на фотографиях
Пошаговое объяснение:
10) нужно было привести q и сделать уравнение
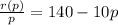
11) нужно представить рабочих в виде дроби (время)
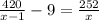 , так как первый рабочий затрачивает на 9 часов меньше, чем второй
, так как первый рабочий затрачивает на 9 часов меньше, чем второй
12) необходимо найти экстремумы функции в данном отрезке через первую производную. Так как функция представлена в виде перемножения 2 функций, то используем формулу y'=(u)'(v)'=u'v + v'u
Потом находим подходящее значение функции, которое должно находится между 5 и 14 по аргументу (x). После этого подставляем подходящее (10) в уравнение ФУНКЦИИ и находим значение y, которое равно 3. Получается что график функции будет выпуклым вниз на участке [5;14] в значении x = 10, а значении y = 3.




ответ: 27.
Пошаговое объяснение:
Наибольшее значение x будет достигаться в том случае, когда сумма справа будет наименьшей. Так как 1/m+1/n=(m+n)/(m*n), а m=18-n, то 1/m+1/n=18/(18*n-n²). Очевидно, что сумма будет наименьшей, если знаменатель дроби будет наибольшим. Таким образом, задача сводится к нахождению наибольшего значения выражения f(n)=18*n-n². Производная f'(n)=18-2*n обращается в ноль при n=9. Так как при n<9 f'(n)>0, то при 1≤n≤8 функция f(n) возрастает. Так как при n>9 f'(n)<0, то при 10≤n≤17 функция f(n) убывает. А это значит, что при n=9 функция f(n) действительно принимает наибольшее значение, которое равно f(9)=18*9-9²=81. Так как при n=9 m=18-9=9, то 6/x=2/9. Отсюда x=27. ответ: 27.
x=26
Пошаговое объяснение:
log5(x-1)=2
x>1
x-1=5^2
x=25+1=26
X=26