Question

Одиннадцатиклассник Виктор твёрдо решил поступить на математический факультет любимого вуза. Виктор пообещал себе, что даже если не сдаст ЕГЭ на необх. одимый , то и дальше каждый год будет сдавать экзамен до тех пор, пока не сможет поступить. Виктор прекрасно понимает, что шанс поступить сразу после окончания школы равен 0,7, а в каждый последующий год вероятность успешного поступления будет равна 0,4. Какое наименьшее число попыток сдачи экзаменов потребуется для того, чтобы вероятность поступления в любимый вуз была не менее 99%?

Answer 1

8

Пошаговое объяснение:

Найдём вероятность того, что Виктор не поступит после n > 1 попыток.

Вероятность того, что первая попытка сразу после школы будет неудачной, равна 1 - 0,7 = 0,3, а вероятность неуспешной сдачи каждого экзамена после этого 1 - 0,4 = 0,6.

Тогда вероятность того, что Виктор не поступит после n попыток, равна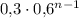 $0{,}3\cdot0{,}6^{n-1}$, а вероятность того, что он поступит, соответственно, $1-0{,}3\cdot0{,}6^{n-1}$.

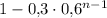Вероятность поступления должна быть не менее 0,99, так что

$0{,}3\cdot0{,}6^{n-1}$

Если верить калькулятору, логарифм в правой части неравенства равен 7,65...., так что наименьшее подходящее n = 8.

Без калькулятора можно построить таблицу значений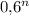 $0{,}6^n$:

$\begin{array}{cc}n & 0.6^n \\1 & 0.6 \\2 & 0.36 \\3 & 0.216 \\4 & 0.1296 \\5 & 0.07776 \\6 & 0.046656 \\7 & 0.0279936 \\\mathbf{8} & \mathbf{0.01679616}\end{array}$

Несколько минут мучений, и получаем, что первое n, при котором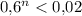 $0{,}6^n$ - это n = 8.