Наименьшее возможное число студентов, так и не сдавших зачет - 32 человека. При этом, первоначально было 242 студента.
Пошаговое объяснение:
Из условия следует, что каждый раз на зачет приходит такое количество студентов, что если к нему добавить еще одного студента, то полученное число делится на три. Тогда:
1 зачет – пришло число студентов А
2 зачет – пришло студентов В, где В связано с А уравнением: В+1 = (2/3) (А+1)
3 зачет – пришло студентов С, где С связано с В уравнением: С+ 1= (2/3)(В+1)
4 зачет – пришло студентов D, где D связано с С уравнением: D+1 = (2/3) (С+1)
5 зачет – пришло студентов Е, где Е связано с D уравнением: E+1 = (2/3) (D+1)
Осталось после 5 подхода студентов F, где F связано с D уравнением F+1= (2/3) (E+1)
Преобразовываем уравнения к виду:
A+1 = (3/2) (B+1) (1)
B+1 = (3/2) (C+1) (2)
C+1 = (3/2) (D+1) (3)
D+1= (3/2) (E+1) (4)
Е+1 = (3/2) (F+1) (5)
И подставляем последовательно уравнения друг в друга, начиная с уравнения (5), получаем:
А+1 = (3/2)^5*(F+1).
Отсюда: А = (243/32)(F+1) – 1 (6)
Уравнение (6) связывает число студентов пришедших на зачет в первый раз (А) с числом студентов, оставшихся после 5 пересдачи (F). Из уравнения (6) видно, что первое целочисленное значение А будет при (F+1) = 32, т.е.
F = 31 и А = 242
В более общем случае можно видеть, что для к подходов для сдачи зачета ответ будет: А=(3/2)^к * (Aк+1) – 1 (для 5 пересдач в нашей задаче, Ак = F и к=5)
Например, для 6 пересдач получим А=(729/64)(А6+1) – 1 и, таким образом А6=63 и А=728.
Пусть х км в час - скорость первого, который шел из А в В.
y км в час - скорость второго, который шел из В в А.
За 5 часов первый х км, второй - 5y км, вместе они км.
Первое уравнение:
После встречи первый шел путь, проийденный вторым до встречи,
т. е 5y км со скоростью (х-1) км в час,
второй - 5х км со скоростью у км в час
По условию первый прибув до пункту В на 2 години раніше, ніж другий - до пункту А.
Второе уравнение:
Решаем систему двух уравнений: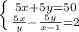
подстановки:
D=73²+4·2·480=5329+3840=9169
√D≈
Проверяйте условие задачи