
(4а⁷b¹⁵-4a⁵b¹⁷)/(2a⁴b⁵-2a⁵b⁴)=-4a⁵b¹⁵*(a²-b²)/(2a⁴b⁴(a-b))=-2ab¹¹*(a+b);
-2*3*(-1)¹¹*(3-1)=6*2=12
Верный ответ А 12
при вынесении общего множителя за скобку выносил множитель с наименьшим показателем, если речь о переменной ; из чисел в числителе вынес 4, в знаменателе 2.
При делении степеней из показателя делимого вычитаем показатель делителя.
При возведении в нечетную степень отрицательного числа получается отрицательное.
При сокращении вынес минус за скобки. при этом поменяв знаки на противоположные.
(а²-b²)/(a-b)=(a-b)(a+b)/(a-b)=(a+b) - сократил устно.
Сразу приступить к вычислению объема прямоугольного параллелепипеда нельзя, так как неизвестны его длина и ширина.
Найдем длину, воспользовавшись тем, что она в 1 7/8 больше ширины:
1) 10 2/3 * 1 7/8 = 32/3 * 15/8 = 20 (см) - длина прямоугольного параллелепипеда.
Найдем высоту параллелепипеда, пользуясь тем что она составляет 15 % (0,15) длины:
2) 20 * 0,15 = 3 (см) - высота прямоугольного параллелепипеда.
Теперь можно приступить к вычислению объема:
3) 10 2/3 * 20 * 3 = 32/3 * 20 * 3 = 32 * 20 = 640 (см3) - объем параллелепипеда.
ответ: 640 см3.
площадь трапеции
площадь трапеции равна произведению полусуммы ее оснований на высоту:
s = ((ad + bc) / 2) · bh,
где высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание.
доказательство.

рассмотрим трапецию abcd с основаниями ad и bc, высотой bh и площадью s.
докажем, что s = ((ad + bc) / 2) · bh.
диагональ bd разделяет трапецию на два треугольника abd и bcd, поэтому s = sabd + sbcd. примем отрезки ad и bh за основание и высоту треугольника abd, а отрезки bcи dh1 за основание и высоту треугольника bcd. тогда
sabc = ad · bh / 2, sbcd = bc · dh1.
так как dh1 = bh, то sbcd = bc · bh / 2.
таким образом,
s = ad · bh / 2 + bc · bh = ((ad + bc) / 2) · bh.это можно только с доказательствомПошаговое объяснение:
Пошаговое объяснение:
...=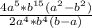 =
=
=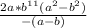 =
=
=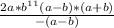 =
=
=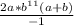 =
=
=-2ab¹¹(a+b).
При a=3 ,b=-1 имеем : -2*3*(-1)¹¹(3-1)=6*2=12