
ответ: 
Пошаговое объяснение:
![\sqrt{12+\sqrt{12+\sqrt[]{20+4x+x^2} } } =x^2+4x+8\\x^2+4x+8 = (x+2)^2+4 = t\geq4 \\\sqrt{12+\sqrt{12+\sqrt[]{12+t} } } = t](/tpl/images/1361/5392/9b8b4.png)
Пусть:
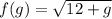
Тогда уравнение принимает вид:
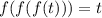
Заметим, что если 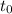 корень уравнения
корень уравнения 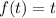 , то он и корень уравнения:
, то он и корень уравнения:
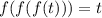 , действительно:
, действительно:
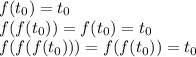
Найдем все такие корни:
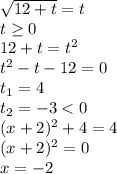
Заметим, что функция 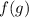 - монотонно возрастает.
- монотонно возрастает.
Предположим, что в уравнении 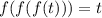 существует корень
существует корень 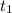 , такой, что
, такой, что 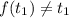
Рассмотрим случай: 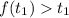 .
.
Поскольку, 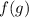 - монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство:
- монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство: 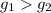 , то верно и данное неравенство:
, то верно и данное неравенство: 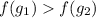
Из данного утверждения следует, что :
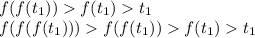
Но 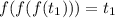 , то есть мы пришли к противоречию.
, то есть мы пришли к противоречию.
Аналогично показывается невозможность утверждения для случая
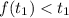 . Таким образом, других корней помимо
. Таким образом, других корней помимо  нет.
нет.
 . Перемножаем крест-накрест и получаем x = 700 – искомое число.
. Перемножаем крест-накрест и получаем x = 700 – искомое число. 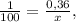

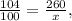
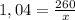
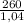 =
= 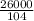
 . Перемножаем крест-накрест и получаем x = 700 – искомое число.
. Перемножаем крест-накрест и получаем x = 700 – искомое число. 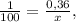

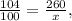
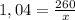
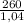 =
= 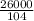
x=-2
Пошаговое объяснение:
Заметим, что левая функция всегда неотрицательная, а у правой функции в неотрицательную область попаает только одна ветвь параболы. (т.к.![\[t \ge 0\]](/tpl/images/1361/5392/8d27e.png) )
)
Значит у функций будет одно пересечение(т.е. одно решение), которое не сложно подобрать при t=4.