∠HPF = 11°.
Объяснение:
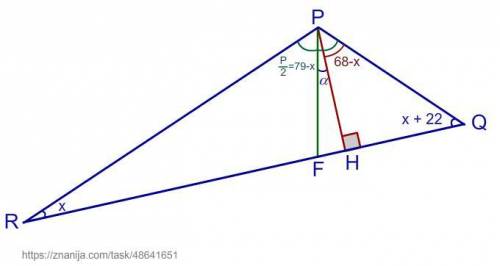
Отрезки PH и PF являются высотой и биссектрисой ΔPQR соответственно. Разность между величинами углов PQR и PRQ равна 22°. Найти угол HPF.
Дано: ΔPQR;
PH - высота;
PF - биссектриса;
∠PQR - ∠PRQ = 22°.
Найти: ∠HPF.
Решение.
1) По условию:
∠PQR - ∠PRQ = 22°.
⇒ ∠PQR = ∠PRQ + 22°.
Пусть ∠PRQ = x, тогда ∠PQR = x + 22°.
Сумма углов в треугольнике равна 180°2) В ΔPQR
∠PRQ = x;
∠PQR = x + 22°;
∠QPR = 180° - x - (x + 22°) = 180° - x - x - 22° = 158 - 2x.
Биссектриса угла в треугольнике - это луч, с началом в вершине угла и делящий угол пополам.3) По условию PF - биссектриса.
∠FPR = ∠QPF = ∠QPR : 2 = (158 - 2x) : 2 = 79 - x.
4) PH - высота по условию.
ΔQPH прямоугольный. ∠PHQ = 90°, ∠PQH = x + 22°,
⇒ ∠QPH = 90° - (x + 22°) = 90° - x - 22° = 68° - x.
5) Для удобства обозначим угол между биссектрисой и высотой α.
∠HPF = α.
∠α = ∠QPF - ∠QPH;
∠α = 79 - x - (68 - x) = 79 - x - 68 + x = 11°
∠HPF = 11°.
Угол между биссектрисой и высотой равен 11°.
Первое уравнение:
Решение через действительные корни:
1. Разделите обе стороны уравнения на два:
х²+2х+16=0
2. Определите коэффициенты квадратного уравнения a,b и с:
а=1,b=2,с=16
3. Подставьте а=1,b=2,с=16 в формулу для вычисления корней квадратного уравнения:
х=-2±√2²-4*1*16:2*1
4. Любое выражение, умноженное на один, не изменяется:
х=-2±√2²-4*16:2
5. Вычислите степень:
х=-2±√4-4*16:2
6. Умножьте числа:
х=-2±√4-64:2
7. Вычислите разность:
х=-2±√-60:2
8. Квадратный корень из отрицательного числа не существует на множестве действительных чисел:
ответ: х∉R (нет действительных корней)
Решение через комплексные корни:
1. Разделите обе стороны уравнения на два:
х²+2х+16=0
2. Определите коэффициенты квадратного уравнения a,b и с:
а=1,b=2,с=16
3. Подставьте а=1,b=2,с=16 в формулу для вычисления корней квадратного уравнения:
х=-2±√2²-4*1*16:2*1
4. Любое выражение, умноженное на один, не изменяется:
х=-2±√2²-4*16:2
5. Вычислите степень:
х=-2±√4-4*16:2
6. Умножьте числа:
х=-2±√4-64:2
7. Вычислите разность:
х=-2±√-60:2
8. Упростите корень:
х=-2±2√15i:2
9. Запишите два решения:одно со знаком плюс и одно со знаком минус:
a)х=-2+2√15i:2
b)х=-2-2√15i:2
10. Упростите оба выражения:
a) -1+√15i:2
b) -1-√15i:2
11. Уравнение имеет два решения:
х¹= -1+√15i:2, х²=-1-√15i:2
Через дискриминант:
1. Определите коэффициенты квадратного уравнения a,b и с:
а=2, b=4, с=32
2. Вычислите дискриминант путем подстановки а=2, b=4, с=32 в выражение b²-4ас:
4²-4*2*32
3. Упростите выражение:
ответ:-240
Второе уравнение:
Решение через действительные корни:
1. Используя (a+b)²=а²+2аb+b², запишите выражение в развёрнутом виде:
x²+10х+25+(х+7)*(х+7)=6х-19
2. Множитель х+7 повторяется два раза, следовательно основание х+7 принимает вторую степень:
х²+10х+25+(х+7)²=6х-19
3. Используя (a+b)²=а²+2аb+b², запишите выражение в развёрнутом виде:
х²+10х+25+х²+14х+49=6х-19
4. Привести подобные члены:
2х²+24х+25+49=6х-19
5. Сложите числа:
2х²+24х+74=6х-19
6. Переместить выражение в левую часть и изменить его знак:
2х²+24х+74-6х-19 =0
7. привести подобные члены:
2х²+18х+74+19=0
8. сложите числа:
2х²+18х+93=0
9. Определите коэффициенты квадратного уравнения a,b и с:
а=2, b=18, с=93
10. подставьте а=2, b=18, с=93 в формулу для вычисления корней квадратного уравнения:
х=-18±√18²-4*2*93:2*2
11. вычислите степень:
х=-18±√324-4*2*93:2*2
12. вычислите произведение:
х=-18±√324-744:4
13. вычислите разность:
х=-18±√-420:4
14. Квадратный корень из отрицательного числа не существует на множестве действительных чисел:
ответ: х∉R (нет действительных корней)
решение через комплексные корни:
1. Используя (a+b)²=а²+2аb+b², запишите выражение в развёрнутом виде:
x²+10х+25+(х+7)*(х+7)=6х-19
2. Множитель х+7 повторяется два раза, следовательно основание х+7 принимает вторую степень:
х²+10х+25+(х+7)²=6х-19
3. Используя (a+b)²=а²+2аb+b², запишите выражение в развёрнутом виде:
х²+10х+25+х²+14х+49=6х-19
4. Привести подобные члены:
2х²+24х+25+49=6х-19
5. Сложите числа:
2х²+24х+74=6х-19
6. Переместить выражение в левую часть и изменить его знак:
2х²+24х+74-6х-19 =0
7. привести подобные члены:
2х²+18х+74+19=0
8. сложите числа:
2х²+18х+93=0
9. Определите коэффициенты квадратного уравнения a,b и с:
а=2, b=18, с=93
10. подставьте а=2, b=18, с=93 в формулу для вычисления корней квадратного уравнения:
х=-18±√18²-4*2*93:2*2
11. вычислите степень:
х=-18±√324-4*2*93:2*2
12. вычислите произведение:
х=-18±√324-744:4
13. вычислите разность:
х=-18±√-420:4
14. Упростите корень:
х=-18±2√105i:4
15. Запишите два решения:одно со знаком плюс и одно со знаком минус:
a) х=-18+2√105i:4
b) х=-18-2√105i:4
16. Упростите выражения:
a) -9/2+√105/2i
b) -9/2-√105/2i
17. Уравнение имеет два решения:
х¹=-9/2+√105/2i, х²=-9/2-√105/2i
решение через дискриминант:
1. запишите квадратное уравнение в стандартном виде:
2х²+18х+93=0
2. 2. Определите коэффициенты квадратного уравнения a,b и с:
а=1,b=2,с=16
3. вычислите дискриминант путем подстановки а=1,b=2,с=16 в выражение b²-4ас:
18²-4*2*93
4. упростите выражение:
ответ:-420.




1)h<1500
2)S>1000
3)R>10000
4)N>=7