1) припустимо, що площа першої ділянки становить х га.
2) тоді 0,4 х га становить площу другої ділянки і (х + 17) га — площа третьої ділянки.
3) (х + 0,4 х + (х + 17)) га-Загальна площа цих трьох земельних ділянок, що за умовою завдання становить 833 га. тому можливо записати:
х + 0,4 х + (х + 17) = 833.
4) вирішимо рівняння:
х + 0,4 х + х + 17 = 833;
2,4 х + 17 = 833;
2,4 х = 833 - 17;
2,4 х = 816;
х = 816 : 2,4;
х = 340.
5) знаходимо, що площа першої ділянки дорівнює 340 га.
6) обчислимо площі інших ділянок:
340 * 0,4 = 136 га — другого;
340 + 17 = 357 га — третього.
Відповідь: 340 га; 136 га і 357 га.
Пошаговое объяснение:
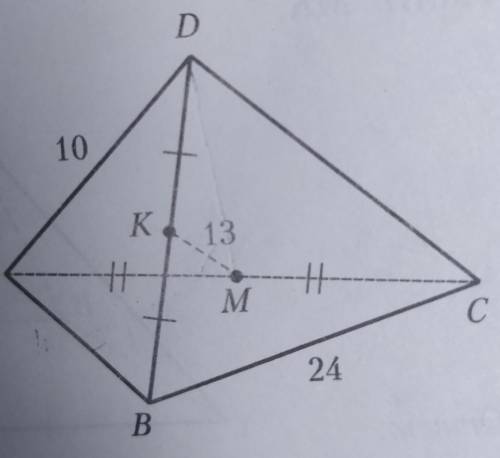
Судя по описаниям, мы имеем тетраэдр ABCD в основании которого лежит правильный треугольник со стороной 24 и сторонами в виде равнобедренных треугольников в боковыми сторонами в 10.
Итак, мы имеем две плоскости ABC и ADC, которые пересекаются и образуют прямую AC. Через точки B и D проведена другая прямая, пересекающая плоскости. Мы должны найти угол между прямыми AС и BD - скрещивающимися.
Рассмотрим углы между этими прямыми в плоскостях ABC и ADC.
Прямая AC лежит в обоих плоскостях.
Проекция BD на плоскость ABC - есть прямая BM. AM = MC -> Угол между BM и AC = 90 градусов.
Проекция BD на плоскость ABC - есть прямая DM. AM = MC -> Угол между DM и AC = 90 градусов.
Углы обеих проекций каждой плоскости и прямой AC составляют 90 градусов. Значит исходная прямая BD и прямая AC составляют угол 90 градусов.
Если ответ удовлетворил, не забудь отметить его как "Лучший".