∠BCA = 40°.
Пошаговое объяснение:
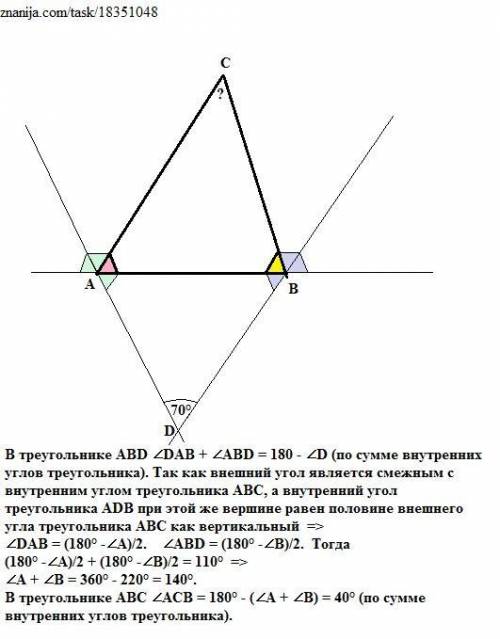
В треугольнике ABD ∠DAB + ∠ABD = 180 - ∠D (по сумме внутренних углов треугольника). Так как внешний угол является смежным с внутренним углом треугольника АВС, а внутренний угол треугольника ADB при этой же вершине равен половине внешнего угла треугольника АВС как вертикальный =>
∠DAB = (180° -∠A)/2. ∠ABD = (180° -∠B)/2. Тогда
(180° -∠A)/2 + (180° -∠B)/2 = 110° =>
∠A + ∠B = 360° - 220° = 140°.
В треугольнике АВС ∠АСВ = 180° - (∠A + ∠B) = 40° (по сумме внутренних углов треугольника).
В заданном выражении (x^2-4x+11)^2-2 определим вершину параболы
хо = -в/2а = -(-4)/2*1 = 2.
В этой точке минимальное значение функции.
у = (2² - 4*2 + 11)² - 2 = 7² - 2 = 47.
ответ: 47.