
![D[f(x)] \in \left[\dfrac{\pi}{3}, \pi \right]](/tpl/images/0746/9641/51b8b.png)
Пошаговое объяснение:
Сначала разберёмся с базовыми областью определения 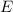 и множеством значений
и множеством значений 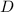 арккосинуса:
арккосинуса:
Арккосинус принимает значения только от -1 до +1: ![E[\arccos{x}] \in [-1, 1]](/tpl/images/0746/9641/a74cb.png) .
.
Арккосинус -- монотонная функция, которая достигает в краевых точка следующих значений: 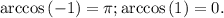 Значит множество значений арккосинуса не может выходить следующих рамок:
Значит множество значений арккосинуса не может выходить следующих рамок:
![D[\arccos{x}] \in [0, \pi]](/tpl/images/0746/9641/c49aa.png)
Далее, перейдём к нашей функции 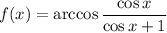 . Для того, чтобы понять, какие значения может иметь данная функция, нужно понять, какие значения может иметь функция
. Для того, чтобы понять, какие значения может иметь данная функция, нужно понять, какие значения может иметь функция 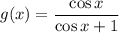 . Так как
. Так как ![E[f(x)] = D[g(x)]](/tpl/images/0746/9641/00b58.png) .
.
У функции 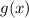 существуют асимптоты
существуют асимптоты 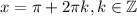 , при приближении к которым функция стремится к
, при приближении к которым функция стремится к 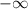 (решение уравнения
(решение уравнения 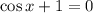 ). Значит нам уже понятно, что минимальное значение функции
). Значит нам уже понятно, что минимальное значение функции 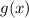 стремится к минус бесконечности.
стремится к минус бесконечности.
Найдём экстремальные точки функции 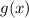 (на самом деле максимальные, но желательно это формально доказать). Для этого приравняем производную
(на самом деле максимальные, но желательно это формально доказать). Для этого приравняем производную 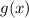 к 0.
к 0.
Найдём 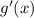 :
:
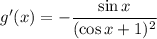
Найдём экстремальные точки 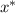 :
:

Принимая во внимание ОДЗ, решением остаются точки 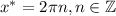 .
.
Эти точки являются экстремальными. Докажем, что они являются максимумами. Для этого найдём вторую производную 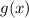 :
:
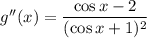
В числителе стоит всегда отрицательная величина, в знаменателе -- всегда положительная. Значит, 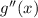 всегда отрицательна. Отсюда следует, что функция
всегда отрицательна. Отсюда следует, что функция 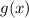 является вогнутой, и для неё ВСЕ экстремальные точки являются максимумами.
является вогнутой, и для неё ВСЕ экстремальные точки являются максимумами.
Значит 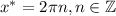 -- максимумы.
-- максимумы.
Значения функции в этих точках: 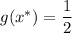
Получается, что ![D[g(x)] \in \left(-\infty, \dfrac{1}{2} \right ]](/tpl/images/0746/9641/6c000.png) .
.
То есть область определения 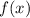 следующая:
следующая:
![E[f(x)] \in \left( -\infty, \dfrac{1}{2} \right]](/tpl/images/0746/9641/44fca.png) .
.
Однако мы знаем, что область определения арккосинуса не может выходить за пределы ![[-1, 1]](/tpl/images/0746/9641/4da46.png) . Значит придётся пересечь эти множества и в итоге окажется:
. Значит придётся пересечь эти множества и в итоге окажется:
![E[f(x)] \in \left[ -1, \dfrac{1}{2} \right]](/tpl/images/0746/9641/a27b3.png) .
.
Так как 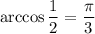 , то множество значений получается следующим:
, то множество значений получается следующим:
![D[f(x)] \in \left[\dfrac{\pi}{3}, \pi \right]](/tpl/images/0746/9641/51b8b.png)
где S - расстояние (пройденный путь), t - время движения и V - скорость.
Рассматриваемые поезда начали движение одновременно и двигались одинаковое количество времени t=10 часов, но с разными скоростями — V1=75 км\час, V2=(75+10)=85 км\час. Тогда расстояние, пройденное поездами: S1=V1*t=75*10=750 км; S2=V2*t=85*10=850 км, откуда следует, что оба поезда встретились и разъехались, проехав каждый более 720 км, причём поезд, который ехал со скоростью 75 км\час, проехав станцию отправления второго поезда, через 10 часов отъехал от неё на 750-720=30 км, а ехавший ему навстречу со скоростью 85 км\час, соответственно проехав пункт отправления, через 10 часов отдалился от неё на 850-720=130 км. Просуммировав все расстояния, получаем расстояние между поездами через 10 часов ходу 130+720+30=880 км. Наглядно — на приложенном рис.