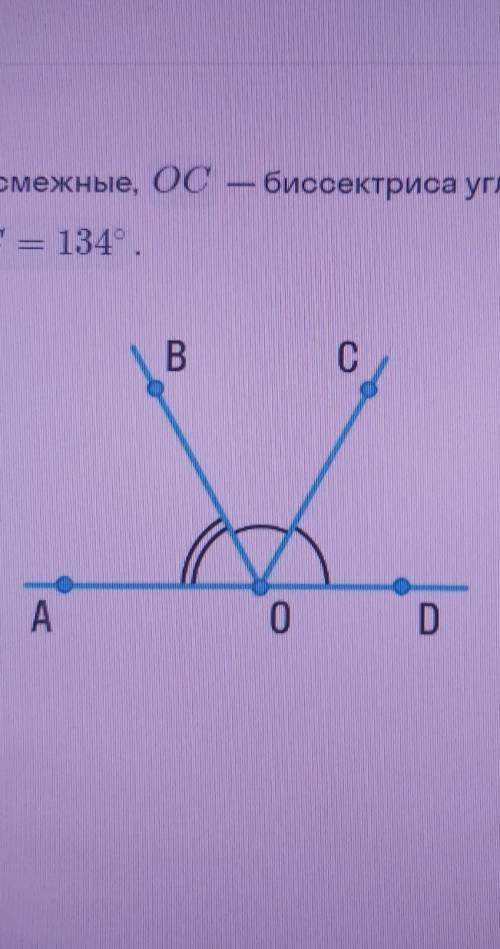
ответ: ∠AOB=88°
Пошаговое решение:
∠СОD=180°-∠AOC=180°-134°=46°
∠BOD=2∠СОD=2*46°=92°
∠AOB=180°-92°=88°
ответ:Область определения функции - это все значения, которые может принимать переменная х.
В уравнении у = √(х^2 - 4х + 3) под знаком корня может быть только положительное число и 0, т.к. нельзя извлечь квадратный корень из отрицательного числа.
x^2 - 4x + 3 ≥ 0 – решим методом интервалов;
найдем нули функции:
x^2 – 4x + 3 = 0;
D = b^2 – 4ac;
D = (- 4)^2 – 4 * 1 * 3 = 16 – 12 = 4; √D = 2;
x = (- b ± √D)/(2a);
x1 = (4 + 2)/2 = 6/2 = 3;
x2 = (4 – 2)/2 = 2/2 = 1.
Отметим на числовой прямой точки 1 и 3, они поделят прямую на три интервала: 1) (- ∞; 1], 2) [1; 3], 3) [3; + ∞). Найдем значение выражения x^2 – 4x + 3 в каждом интервале. В ответ выпишем те интервалы, в которых оно положительно.
Пошаговое объяснение:
Пошаговое объяснение:Так как углы AOB и BOD - смежные, то они равны 180°. Тогда BOD = 180-108; BOD = 72°. Биссектриса угла BOD = 72:2; OC = 36°, значит угол BOC=72°.
ответ: BOC=72°