С двух сторон кубиков окрашено:
берем количество ребер к большого куба (12),
считаем на сколько частей разделили каждое ребро (раз 1 дм =10 см, то каждое ребро содержит по 10 кубиков), отнимем все угловые кубики, и ребро без угловых кубиков содержит по 8 кубиков. 8 * 12 = 96.
ответ: с двух сторон окрашено 96 кубиков
С одной стороны:
считаем сколько мелких кубиков у куба в каждой грани (10*10),
вычитаем угловые (4 для каждой грани) и рёберные (у каждой грани 4 ребра, а в каждом ребре по 8 кубиков, поэтому 4*8) кубики и умножаем на число граней у куба (6):
(10*10-4-8*4) * 6 = 384
С двух сторон кубиков окрашено:
берем количество ребер к большого куба (12),
считаем на сколько частей разделили каждое ребро (раз 1 дм =10 см, то каждое ребро содержит по 10 кубиков), отнимем все угловые кубики, и ребро без угловых кубиков содержит по 8 кубиков. 8 * 12 = 96.
ответ: с двух сторон окрашено 96 кубиков
С одной стороны:
считаем сколько мелких кубиков у куба в каждой грани (10*10),
вычитаем угловые (4 для каждой грани) и рёберные (у каждой грани 4 ребра, а в каждом ребре по 8 кубиков, поэтому 4*8) кубики и умножаем на число граней у куба (6):
(10*10-4-8*4) * 6 = 384
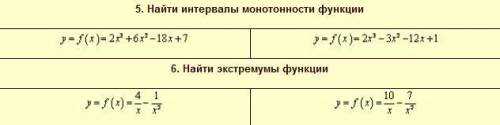
1. найдем производную. 6х²-12х-18=6*(х²-2х-3), найдем критические точки. 6*(х²-2х-3)=0, по Виету х=-1; х=3
-13
+ - +
функция возрастает при х∈(-∞;-1] и при х∈ [3;+∞), и убывает при х∈ [-1;3]
2 производная равна 6х²-6х-12=0; 6(х²-х-2)=0; по Виету х=2; х=-1
-12
+ - +
функция возрастает при х∈(-∞;-1] и при х∈ [2;+∞), и убывает при х∈ [-1;2]
3.производная равна -4/х²+2/х³=(2-4х)/х³; х=0; х=0.5
00.5
- + -
х=0.5- точка максимума, максимум равен 4/(1/2)-1/(1/2)²=8-4=4
4. производная равна -10/х²+14/х³=0, 14-10х=0; х=1.4
01.4
- + -
х=х=1.4- точка максимума, максимум равен 10/(1.4)-1/(1.4)²=1300/196=
315/49