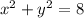 — уравнение окружности с центром
— уравнение окружности с центром 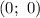 и радиусом
и радиусом 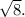
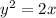 — уравнение параболы
— уравнение параболы
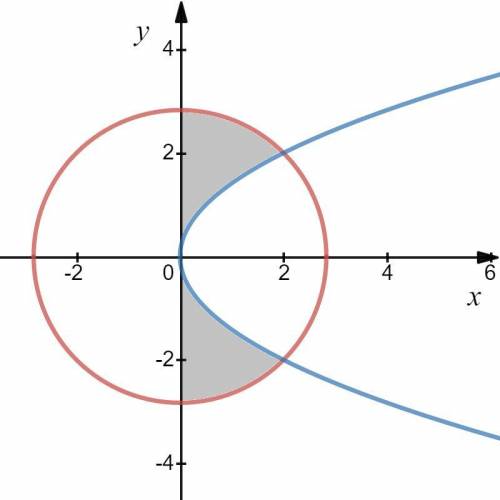
Изобразим графики данных уравнений и найдем площадь образовавшейся фигуры в правой полуплоскости.
Выразим ординаты данных уравнений:
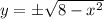 и
и 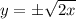
Так как имеем симметричные фигуры, найдем площадь 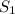 одной из них. Общая их площадь
одной из них. Общая их площадь 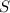 будет состоять из площади двух
будет состоять из площади двух 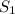 , то есть
, то есть 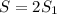
Тогда 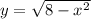 и
и 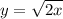 . Поэтому
. Поэтому 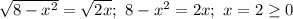
Так как окружность вытесняет больше площади, чем парабола, то имеем разность их площадей, определяющаяся через определенный интеграл:
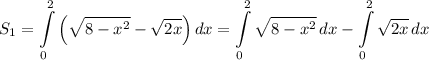
Найдем первый интеграл геометрически: площадь круга находится по формуле 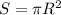 , где
, где 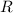 — радиус круга. Тогда четверть круга:
— радиус круга. Тогда четверть круга: 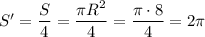
Найдем второй интеграл по формуле Ньютона-Лейбница:
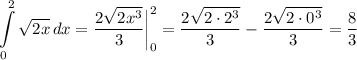
Таким образом, 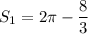 кв. ед.
кв. ед.
Тогда 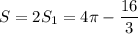 кв. ед.
кв. ед.
ответ: 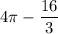 кв. ед.
кв. ед.
Задание 2
Составьте простой план и напишите текст (объем письменной работы 100-150 слов) на одну из предложенных тем. В письменную работу включите предложения с прямой речью.
1. Придумайте и напишите сказку для младших школьников о том, как появился первый космический корабль.
2. Напишите письмо своему другу (подруге), в котором пригласите его (ее) совместно посетить выставку современных автомобилей. Расскажите в письме о том, какие автомобили будут представлены на выставке.
3. Представьте, что вы участник праздника «День языков народа Казахстана». Напишите в своем дневнике, что происходило в этот день. Постарайтесь передать ваши чувства, эмоции, настроение.
4. Напишите рекламный текст для учащихся об открытии «Школы иностранных языков». Постарайтесь убедить школьников записаться в школу и обязательно посещать занятия.