Примерная схема исследования функции с целью построения ее графика имеет следующую структуру:
1) Область определения и область допустимых значений функции. Нет ограничений: D(x) = R. 2) Четность, нечетность функции. y(-x)= -x^3+4. значит, функция не является ни чётной. ни нечётной. 3) Точки пересечения с осями. Точки пересечения с осью X (Y = 0): x³ = -4 Аналитическое решение x1= ∛4. Численное решениеx1=−1.58740105197. График пересекает ось Y, когда x равняется 0: подставляем x = 0 в x^3 + 4. f(0) = 0³+4 = 4.Точка: (0, 4)4) Асимптоты функции. Горизонтальной и наклонной асимптот не существует. 5) Экстремумы и интервалы монотонности. Находим производную: f'(x) = 3x². Так как х в квадрате, то производная только положительна. Отсюда вывод - у функции нет экстремумов и она только возрастающая. 6) Точки перегиба и промежутки выпуклости, вогнутости. Находим вторую производную и приравниваем нулю: f''(x) = 6x = 0, x = 0. Перегиб в точке х = 0. 7) Сводная таблица и график - в приложении.
Правильная четырехугольная пирамида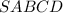 .
.
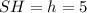 (см).
(см).
Найти: - сторону основания.
- сторону основания.
Решение:Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
Попробуем выразить через
через  (сторону основания) и
(сторону основания) и 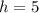 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный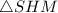 (где
(где 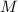 - середина
- середина 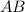 ). В нем
). В нем 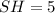 (см), а
(см), а 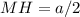 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что - неотрицательное):
- неотрицательное):
Пусть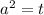 :
:
Второй корень нам не подходит по причине отрицательности. Значит:
Задача решена!
ответ: